题目内容
【题目】如图,甲、乙两只捕捞船同时在上午![]() 从
从![]() 港出海捕鱼.甲船以
港出海捕鱼.甲船以![]() 的速度沿西偏北
的速度沿西偏北![]() 方向前进,乙船以
方向前进,乙船以![]() 的速度沿东北方向前进.甲船在
的速度沿东北方向前进.甲船在![]() 航行到达
航行到达![]() 处,此时甲船发现部分渔具丢在乙船上,于是甲船快速(匀速)沿北偏东
处,此时甲船发现部分渔具丢在乙船上,于是甲船快速(匀速)沿北偏东![]() 的方向追赶,结果两船在
的方向追赶,结果两船在![]() 处相遇.(其他因素不作考虑)
处相遇.(其他因素不作考虑)
![]() 问乙船在什么时候被甲船追上;
问乙船在什么时候被甲船追上;
![]() 求甲船追赶乙船的速度.
求甲船追赶乙船的速度.
【答案】(1)乙船在![]() 被甲船追上;(2)甲船追赶乙船的速度是每小时(15+15
被甲船追上;(2)甲船追赶乙船的速度是每小时(15+15![]() )千米.
)千米.
【解析】
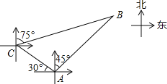
(1)根据方向角可以得到∠BCA=45°,∠B=30度,过A作AD⊥BC于点D,在直角△ACD中,根据三角函数就可求得AD的长,再在直角△ABD中,根据三角函数即可求得AB的长,就可求得时间;
(2)求出BC的长,根据(1)中的结果求得时间,即可求得速度.
(1)如图,过A作AD⊥BC于点D.作CG∥AE交AD于点G.
∵乙船沿东北方向前进,∴∠HAB=45°.
∵∠EAC=30°,∴∠CAH=90°﹣30°=60°,∴∠CAB=60°+45°=105°.
∵CG∥EA,∴∠GCA=∠EAC=30°.
∵∠FCD=75°,∴∠BCG=15°,∠BCA=15°+30°=45°,∴∠B=180°﹣∠BCA﹣∠CAB=30°.
在直角△ACD中,∠ACD=45°,AC=2×15![]() 30
30![]() .
.
AD=ACsin45°=30![]() 30.
30.
CD=ACcos45°=30.
在直角△ABD中,∠B=30°,则AB=2AD=60.
则甲船从C处追赶上乙船的时间是:60÷15﹣2=2(小时).
答:乙船在![]() 被甲船追上.
被甲船追上.
(2)BC=CD+BD=30+30![]() .
.
则甲船追赶乙船的速度是每小时(30+30![]() )÷(4-2)=15+15
)÷(4-2)=15+15![]() (千米/时).
(千米/时).
答:甲船追赶乙船的速度是每小时(15+15![]() )千米.
)千米.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目