题目内容
【题目】如图,在ABCD中,点E,F在对角线AC上,且AE=CF.求证: 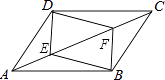
(1)DE=BF;
(2)四边形DEBF是平行四边形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAE=∠BCF,
在△ADE和△CBF中,

∴△ADE≌△CBF,
∴DE=BF
(2)证明:由(1),可得△ADE≌△CBF,
∴∠ADE=∠CBF,
∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,
∴∠DEF=∠BFE,
∴DE∥BF,
又∵DE=BF,
∴四边形DEBF是平行四边形
【解析】(1)根据全等三角形的判定方法,判断出△ADE≌△CBF,即可推得DE=BF.(2)首先判断出DE∥BF;然后根据一组对边平行且相等的四边形是平行四边形,推得四边形DEBF是平行四边形即可.
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.

练习册系列答案
相关题目
【题目】老师想知道某校学生每天上学路上要花多少时间,于是随机选取30名同学每天来校的大致时间(单位:分钟)进行统计,统计表如下:
时间 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 45 |
人数 | 3 | 3 | 6 | 12 | 2 | 2 | 1 | 1 |
(1)写出这组数据的中位数和众数;
(2)求这30名同学每天上学的平均时间.