题目内容
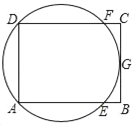
【题目】矩形Ⅰ的面积为6，矩形Ⅱ中的三条边总长为6，则下列说法不正确的是（ ）
A.矩形Ⅰ中一组邻边的长满足反比例函数关系
B.矩形Ⅰ中一组邻边的长可能是3+
和3﹣
C.矩形Ⅰ的周长不可能是8
D.矩形Ⅱ的最大面积是3
【答案】D
【解析】
矩形的面积是两条邻边的积为6，因此邻边成反比例关系，以3+
和3﹣为一组邻边的矩形的面积为（3+）（3﹣）＝9﹣3＝6，假设矩形Ⅰ的周长是8，利用方程求边长，若存在说明周长可以为8，否则不能为8；设矩形Ⅱ的邻边的长，建立面积与边长之间函数关系，利用函数的最值得出结论．
解：①设矩形Ⅰ的一边长为x，与其相邻的边为y，则xy＝6，即y＝
，因此A选项是正确的，
②以3+和3﹣为一组邻边的矩形的面积为（3+）（3﹣）＝9﹣3＝6，因此B选项是正确的，
③当矩形Ⅰ的周长是8时，设一边为x，则邻边为（4﹣x），由面积得：x（4﹣x）＝6，即：x2﹣4x+6＝0，此方程无实数根，因此周长不能为8，故C是正确的，
④设矩形Ⅱ的一组对边长为x，则邻边为6﹣2x，则面积S＝x（6﹣2x）＝﹣2x2+6x，当x＝1.5时，S最大＝4.5，因此D是错误的，
故选：D．
阳光课堂课时优化作业系列答案
【题目】某校门口竖着“前方学校，减速慢行”的交通指示牌CD，数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动，他们定好了如下测量方案：
项目 | 内容 |
课题 | 测量交通指示牌CD的高度 |
测量示意图 |
|
测量步骤 | (1)从交通指示牌下的点M处出发向前走10 米到达A处； (2)在点A处用量角仪测得∠DAM＝27°； (3)从点A沿直线MA向前走10米到达B处；(4)在点B处用量角仪测得∠CBA＝18°． |
请你帮助该小组同学根据上表中的测量数据，求出交通指示牌CD的高度．(参考数据sin27°≈0.45，cos27°≈0.89，tan27°≈0.51，sin18°≈0.31，cos18°≈0.95，tan18°≈0.32)
