题目内容
甲、乙两位同学对问题“求代数式y=x2+
的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成y=(x+
)2-2,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成y=(x-
)2+2,最小值为2”.你认为( )
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| A、甲对 | B、乙对 |
| C、甲、乙都对 | D、甲乙都不对 |
分析:先用配方法得到y=(x-
)2+2和y=(x-
)2+2,再根据x和
一定同号判断出正确的解析式.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答:解:因为x和
一定同号,不可能出现x=-
的情况.
所以 x+
≠0.
所以 乙正确.
故选:B.
| 1 |
| x |
| 1 |
| x |
所以 x+
| 1 |
| x |
所以 乙正确.
故选:B.
点评:本题考查了配方法的应用.此题注意x和
的关系:互为倒数,显然它们的平方和只有在都是1或-1时,有最小值.
| 1 |
| x |

练习册系列答案
相关题目
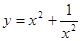 的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成
的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成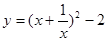 ,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成
,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成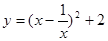 ,最小值为2”.你认为( )
,最小值为2”.你认为( )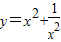 的最小值”提出各自的想法.甲说:“可以用配方法,把它配成
的最小值”提出各自的想法.甲说:“可以用配方法,把它配成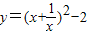 ,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成
,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成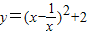 ,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.
,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.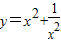 的最小值”提出各自的想法.甲说:“可以用配方法,把它配成
的最小值”提出各自的想法.甲说:“可以用配方法,把它配成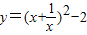 ,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成
,所以函数的最小值为-2”.乙说:“我也用配方法,但我配成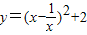 ,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.
,最小值为2”.你认为 (填写“甲对”,“乙对”,“甲,乙都对”或“甲乙都不对”)的.你还可以用 法等方法来解决.