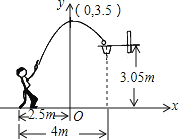
��Ŀ����
����Ŀ����ͼ����PΪx���������ϵ�һ���㣬����P��x��Ĵ��ߣ�������![]() ��ͼ���ڵ�A��������
��ͼ���ڵ�A��������![]() ��ͼ���ڵ�B������B��x���ƽ���ߣ���
��ͼ���ڵ�B������B��x���ƽ���ߣ���![]() �ڵ�C���߽�AC��
�ڵ�C���߽�AC��
��1������P������Ϊ��1��0��ʱ������ABC�������
��2������P������Ϊ��1��0��ʱ����y�����Ƿ����һ��Q��ʹA��O��Q����Ϊ�������������QAOΪ���������Σ������ڣ���ֱ��д��Q������ꣻ�������ڣ�˵�����ɣ�
��3����������OA��OC������P������Ϊ��t��0��ʱ����OAC������Ƿ���t��ֵ�ı仯���仯����˵�����ɣ�
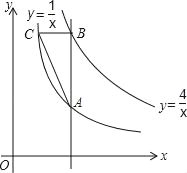
���𰸡���1��![]() ����2����Q������Ϊ��0����
����2����Q��������0����![]() ������0��
������0��![]() ������0��2������0��1����
������0��2������0��1����
��3��������.
��������
��1������P�����������A��B�������꣬Ȼ�����C�����꣬�õ�AB=3��BC=![]() �������������������ʽ��⼴�ɣ�
�������������������ʽ��⼴�ɣ�
��2����ͼ���������OA=![]() ���ٷ�OA=OQ��AQ=AO��QO=QA����������ֱ����Q�����꼴�ɣ�
���ٷ�OA=OQ��AQ=AO��QO=QA����������ֱ����Q�����꼴�ɣ�
��3����ͼ������C��CE��x���ڵ�E��CD��y���ڵ�D����Ϊ��P������Ϊ��t��0�������Ե�A������Ϊ��t��![]() ������B��t��
������B��t��![]() ������C��
������C��![]() ��
��![]() ������ͼ����֪S��OAC=S����CDOE+S����APEC��S��OCD��S��OAP�������ɵõ�����t�ķ��̣�Ȼ��ⷽ�̼���.
������ͼ����֪S��OAC=S����CDOE+S����APEC��S��OCD��S��OAP�������ɵõ�����t�ķ��̣�Ȼ��ⷽ�̼���.
�⣺��1������P������Ϊ��1��0��ʱ����A��B�ĺ�����Ϊ1��
����A�ڷ���������y=![]() �ϣ���B�ڷ���������y=
�ϣ���B�ڷ���������y=![]() �ϣ�
�ϣ�
����A��1��1������B��1��4����
��BC��x�ᣬ
����C��������Ϊ4��
������C��y=![]() �ϣ�
�ϣ�
����C��������![]() ��4����
��4����
��AB=3��BC=![]() ��
��
��S��ABC=![]() ��BC��AB=
��BC��AB=![]() ��
��
��2����ͼ����ʾ��OA=![]() =
=![]() ��
��
����OA=OQ����Qλ��Q1��Q2λ�ã���ʱQ1��0����![]() ����Q2��0��
����Q2��0��![]() ����
����
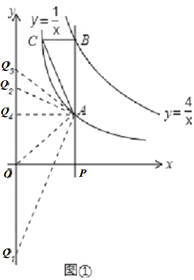
����AQ=AO����Qλ��Q3λ�ã���ʱQ3��0��2����
����QO=QA����Qλ��Q4λ�ã���ʱQ4��0��1����
��Q��������0����![]() ������0��
������0��![]() ������0��2������0��1����
������0��2������0��1����
��3������C��CE��x���ڵ�E��CD��y���ڵ�D����ͼ����ʾ��
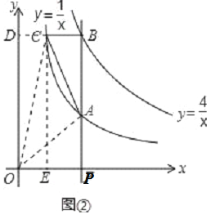
����P��������t��0����
����A��������t��![]() ������B��t��
������B��t��![]() ������C��
������C��![]() ��
��![]() ����
����
��S��OAC=S����CDOE+S����APEC��S��OCD��S��OAP=1+![]() ��
��![]() +
+![]() ������t��
������t��![]() ����
����![]() ��
��![]() =
=![]() ��
��
����OAC���������t��ֵ�ı仯���仯��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�