题目内容
【题目】如图,边长为2的正△ABC的边BC在直线l上,两条距离为l的平行直线a和b垂直于直线l,a和b同时向右移动(a的起始位置在B点),速度均为每秒1个单位,运动时间为t(秒),直到b到达C点停止,在a和b向右移动的过程中,记△ABC夹在a和b之间的部分的面积为s,则s关于t的函数图象大致为( )

A.  B.
B.  C.
C. 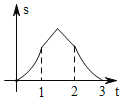 D.
D. 
【答案】B
【解析】
依据a和b同时向右移动,分三种情况讨论,求得函数解析式,进而得到当0≤t<1时,函数图象为开口向上的抛物线的一部分,当1≤t<2时,函数图象为开口向下的抛物线的一部分,当2≤t≤3时,函数图象为开口向上的抛物线的一部分.
如图①,当0≤t<1时,BE=t,DE=![]() t,
t,

∴s=S△BDE=![]() ×t×
×t×![]() t=
t=![]() t2;
t2;
如图②,当1≤t<2时,CE=2-t,BG=t-1,

∴DE=![]() (2-t),FG=
(2-t),FG=![]() (t-1),
(t-1),
∴s=S五边形AFGED=S△ABC-S△BGF-S△CDE=![]() ×2×
×2×![]() -
-![]() ×(t-1)×
×(t-1)×![]() (t-1)-
(t-1)-![]() ×(2-t)×
×(2-t)×![]() (2-t)=-
(2-t)=-![]() t2+3
t2+3![]() t-
t-![]() ;
;
如图③,当2≤t≤3时,CG=3-t,GF=![]() (3-t),
(3-t),

∴s=S△CFG=![]() ×(3-t)×
×(3-t)×![]() (3-t)=
(3-t)=![]() t2-3
t2-3![]() t+
t+![]() ,
,
综上所述,当0≤t<1时,函数图象为开口向上的抛物线的一部分;当1≤t<2时,函数图象为开口向下的抛物线的一部分;当2≤t≤3时,函数图象为开口向上的抛物线的一部分,
故选B.

【题目】为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … |
油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
①根据上表的数据,请你写出Q与t的关系式;
②汽车行驶5h后,油箱中的剩余油量是多少?
③该品牌汽车的油箱加满50L,若以100km/h的速度匀速行驶,该车最多能行驶多远?





