Question

【题目】如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B．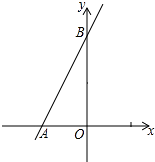

（1）求A、B两点的坐标；
（2）过B点作直线BP与x轴相交于P，且使AP=2OA，求△BOP的面积．

Answer 1

【答案】
（1）

解：当y=0时，2x+3=0，解得x=﹣ ，则A点坐标为（﹣ ，0）；

当x=0时，y=2x+3=3，则B点坐标为（0，3）

（2）

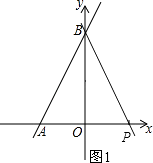
解：当点P在x轴的正半轴上，如图1，

∵AP=2OA，

∴OA=OP，

∴P点坐标为（ ，0），

∴△BOP的面积= 3= ；

当点P在x轴的负半轴上，如图2，

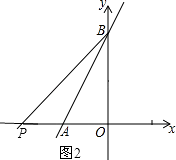
∵AP=2OA，

∴OP=3OA=3 = ，

∴P点坐标为（﹣ ，0），

∴△BOP的面积= 3= ，

综合所述，△BOP的面积为 或

【解析】（1）根据坐标轴上点的坐标特征求A点和B点坐标；（2）分类讨论：当点P在x轴的正半轴上，如图1，由AP=2OA得到OA=OP= ，则P点坐标为（ ，0），然后根据三角形面积公式计算；当点P在x轴的负半轴上，如图2，由AP=2OA得到OP=3OA= ，则P点坐标为（﹣ ，0），然后根据三角形面积公式计算．
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识，掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小．