题目内容
在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作等腰Rt△ADE.
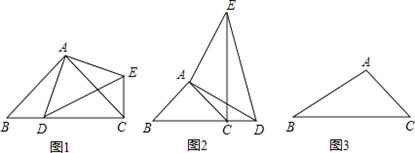
(1)如果AB=AC,∠BAC=90°.解答下列问题:①如图1,当点D在线段BC上时(与点B不重合),线段CE、BD之间的位置关系为 _________ ,数量关系为 _________ .②当点D在线段BC的延长线上时,如图2,线段CE、BD之间的位置关系为 _________ ,数量关系为 _________ .请在上面①②两个结论中任选一个说明理由.
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.试探究:当△ABC满足∠BCA= _________ 时,CE⊥BC(点C、E重合除外)?请在图3中画出相应图形,并说明理由.(画图不写作法)
(1)如果AB=AC,∠BAC=90°.解答下列问题:①如图1,当点D在线段BC上时(与点B不重合),线段CE、BD之间的位置关系为 _________ ,数量关系为 _________ .②当点D在线段BC的延长线上时,如图2,线段CE、BD之间的位置关系为 _________ ,数量关系为 _________ .请在上面①②两个结论中任选一个说明理由.
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.试探究:当△ABC满足∠BCA= _________ 时,CE⊥BC(点C、E重合除外)?请在图3中画出相应图形,并说明理由.(画图不写作法)
解:(1)①CE⊥BD; CE=BD.
证明:∵∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,
∴∠BAD=∠CAE.又 BA=CA,AD=AE,
∴△ABD≌△ACE (SAS)
∴∠ACE=∠B=45°; CE=BD.
∴∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,即 CE⊥BD.
故答案为 CE⊥BD; CE=BD.
②CE⊥BD; CE=BD.理由同①;
(2)如图所示.当∠ACB=45°时,CE⊥BC.
理由:过点A作AP⊥AC交BC边于P.
则∠APC=45°,AP=AC.
∴∠DAP=90°﹣∠DAC,∠EAC=90°﹣∠CAD,
∴∠DAP=∠EAC.
又∵AD=AE,
∴△APD≌△ACE (SAS)
∴∠ACE=∠APD=45°.
∴∠ECB=45°+45°=90°,
即 CE⊥BC.故答案为 45°.
证明:∵∠BAD=90°﹣∠DAC,∠CAE=90°﹣∠DAC,
∴∠BAD=∠CAE.又 BA=CA,AD=AE,
∴△ABD≌△ACE (SAS)
∴∠ACE=∠B=45°; CE=BD.
∴∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,即 CE⊥BD.
故答案为 CE⊥BD; CE=BD.
②CE⊥BD; CE=BD.理由同①;
(2)如图所示.当∠ACB=45°时,CE⊥BC.
理由:过点A作AP⊥AC交BC边于P.
则∠APC=45°,AP=AC.
∴∠DAP=90°﹣∠DAC,∠EAC=90°﹣∠CAD,
∴∠DAP=∠EAC.
又∵AD=AE,
∴△APD≌△ACE (SAS)
∴∠ACE=∠APD=45°.
∴∠ECB=45°+45°=90°,
即 CE⊥BC.故答案为 45°.


练习册系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
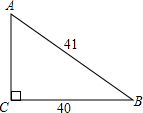 如图,在△ABC中,AC=
如图,在△ABC中,AC=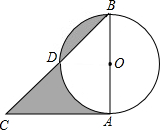 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=