题目内容
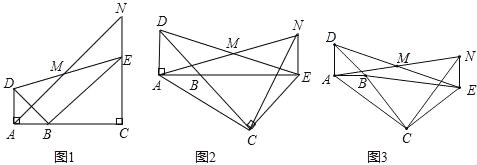
【题目】如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．
（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；
（2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；
（3）将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．
【答案】（1）证明见解析（2）证明见解析（3）△ACN仍为等腰直角三角形
【解析】
试题分析：（1）由EN∥AD和点M为DE的中点可以证到△ADM≌△NEM，从而证到M为AN的中点．
（2）易证AB=DA=NE，∠ABC=∠NEC=135°，从而可以证到△ABC≌△NEC，进而可以证到AC=NC，∠ACN=∠BCE=90°，则有△ACN为等腰直角三角形．
（3）延长AB交NE于点F，易得△ADM≌△NEM，根据四边形BCEF内角和，可得∠ABC=∠FEC，从而可以证到△ABC≌△NEC，进而可以证到AC=NC，∠ACN=∠BCE=90°，则有△ACN为等腰直角三角形．
试题解析：（1）如图1，
∵EN∥AD，
∴∠MAD=∠MNE，∠ADM=∠NEM．
∵点M为DE的中点，
∴DM=EM．
在△ADM和△NEM中，
∴
．
∴△ADM≌△NEM．
∴AM=MN．
∴M为AN的中点．
（2）如图2，
∵△BAD和△BCE均为等腰直角三角形，
∴AB=AD，CB=CE，∠CBE=∠CEB=45°．
∵AD∥NE，
∴∠DAE+∠NEA=180°．
∵∠DAE=90°，
∴∠NEA=90°．
∴∠NEC=135°．
∵A，B，E三点在同一直线上，
∴∠ABC=180°﹣∠CBE=135°．
∴∠ABC=∠NEC．
∵△ADM≌△NEM（已证），
∴AD=NE．
∵AD=AB，
∴AB=NE．
在△ABC和△NEC中，
∴△ABC≌△NEC．
∴AC=NC，∠ACB=∠NCE．
∴∠ACN=∠BCE=90°．
∴△ACN为等腰直角三角形．
（3）△ACN仍为等腰直角三角形．
证明：如图3，延长AB交NE于点F，
∵AD∥NE，M为中点，
∴易得△ADM≌△NEM，
∴AD=NE．
∵AD=AB，
∴AB=NE．
∵AD∥NE，
∴AF⊥NE，
在四边形BCEF中，
∵∠BCE=∠BFE=90°
∴∠FBC+∠FEC=360°﹣180°=180°
∵∠FBC+∠ABC=180°
∴∠ABC=∠FEC
在△ABC和△NEC中，
∴△ABC≌△NEC．
∴AC=NC，∠ACB=∠NCE．
∴∠ACN=∠BCE=90°．
∴△ACN为等腰直角三角形．
