Question

如图，已知∠DAB＋∠D＝180°，AC平分∠DAB，且∠CAD＝35°，∠B＝85°，

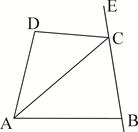
（1）求∠DCE的度数；

（2）求∠DCA的度数.

 

Answer 1

【答案】

（1）85°；（2）35°

【解析】

试题分析：（1）先根据∠DAB+∠D=180°证得DC//AB，再根据平行线的性质求解即可；

（2）先根据角平分线的性质求得∠CAB的度数，再根据平行线的性质求解即可.

（1）∵∠DAB+∠D=180°

∴DC//AB   

∴∠DCE=∠B=85°；

（2）∵AC平分DAB，∠CAD=35°

∴∠CAB=∠CAD=35°

又∵DC//AB

∴∠DCA=∠CAB=35°.

考点：平行线的判定和性质，角平分线的性质

点评：解题的关键是熟练掌握角的平分线把角分成相等的两个小角，且都等于大角的一半.