题目内容
．（本题满分10分）
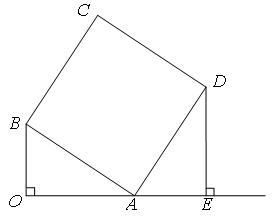
如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．
1.（1）求证：△ADF∽△DEC：
2.（2）若AB=4，AD=3
，AE=3，求AF的长．
1.（1）证明：∵四边形ABCD是平行四边形
∴AD∥BC， AB∥CD，
∴∠ADF=∠CED，∠B+∠C=180°．
∵∠AFE+∠AFD=180，∠AFE=∠B，
∴∠AFD=∠C．
∴△ADF∽△DEC．…………………6分
2.（2）解：∵四边形ABCD是平行四边形，
∴AD∥BC CD=AB=4．
又∵AE⊥BC ，∴ AE⊥AD．
在Rt△ADE中，DE=．
∵△ADF∽△DEC，∴．∴
．AF=
．…………10分
解析:略
练习册系列答案
相关题目
，
）.
的图象的顶点为
．二次函数
的图象与
轴交于原点
及另一点
，它的顶点
在函数
为菱形时，求函数