题目内容
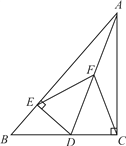
【题目】如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连结EF、CF.
(1)若AD平分∠BAC,求证:EF=CF.
(2)若点F是线段AD的中点,试猜想线段EF与CF的大小关系,并加以证明.
(3)在(2)的条件下,若∠BAC=45°,AD=6,直接写出C、E两点间的距离.
【答案】(1)证明见解析;(2)EF=CF.理由见解析;(3)![]() .
.
【解析】试题分析:(1)由AD平分∠BAC,DE⊥AB,∠ACB=90°可得:∠1 =∠2,∠1+∠3=90°,∠2+∠4=90°,DE= DC,则∠3=∠4,则在△DEF≌△DCF,再根据全等三角形的性质可得出EF=CF;(2)在Rt△AED和Rt△ACD中,由点F是线段AD的中点可得: ![]() ,
, ![]() ,所以EF=CF;(3)由AD=6,EF=CF=
,所以EF=CF;(3)由AD=6,EF=CF=![]() AD=AF=DF=3可得:∠DFE=2∠FAE,∠CFD=2∠CAF,所以∠EFC=2∠CAE=90°,即△CEF是直角三角形,所以CE=
AD=AF=DF=3可得:∠DFE=2∠FAE,∠CFD=2∠CAF,所以∠EFC=2∠CAE=90°,即△CEF是直角三角形,所以CE=![]() ;
;
试题解析:
(1)如图所示:

∵AD平分∠BAC,DE⊥AB,∠ACB=90°,
∴∠1 =∠2,∠1+∠3=90°,∠2+∠4=90°,DE= DC.
∴∠3=∠4.
∵DF = DF,
∴△DEF≌△DCF.
∴EF=CF.
(2)EF=CF. (只写结论给1分)
在Rt△AED和Rt△ACD中,
∵点F是线段AD的中点,
∴![]() ,
, ![]() ,
,
∴EF=CF. \
(3)![]() .
.

练习册系列答案
相关题目