题目内容
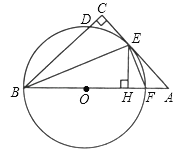
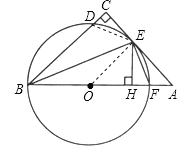
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长.
【答案】(1)证明见解析;(2)证明见解析;(3)BF=10,AF=![]() .
.
【解析】(1)如图,连接OE.
∵BE⊥EF,∴∠BEF=90°,∴BF是圆O的直径.
∵BE平分∠ABC,∴∠CBE=∠OBE,∵OB=OE,∴∠OBE=∠OEB,∴∠OEB=∠CBE,∴OE∥BC,∴∠AEO=∠C=90°,∴AC是⊙O的切线;
(2)如图,连结DE.
∵∠CBE=∠OBE,EC⊥BC于C,EH⊥AB于H,∴EC=EH.
∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,∴∠CDE=∠HFE.
在△CDE与△HFE中,∵∠CDE=∠HFE,∠C=∠EHF,EC=EH,∴△CDE≌△HFE(AAS),∴CD=HF.
(3)由(2)得CD=HF,又CD=1,∴HF=1,在Rt△HFE中,EF=![]() =
=![]() ,∵EF⊥BE,∴∠BEF=90°,∴∠EHF=∠BEF=90°,∵∠EFH=∠BFE,∴△EHF∽△BEF,∴
,∵EF⊥BE,∴∠BEF=90°,∴∠EHF=∠BEF=90°,∵∠EFH=∠BFE,∴△EHF∽△BEF,∴![]() ,即
,即![]() ,∴BF=10,∴OE=
,∴BF=10,∴OE=![]() BF=5,OH=5﹣1=4,∴Rt△OHE中,cos∠EOA=
BF=5,OH=5﹣1=4,∴Rt△OHE中,cos∠EOA=![]() ,∴Rt△EOA中,cos∠EOA=
,∴Rt△EOA中,cos∠EOA=![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴OA=
,∴OA=![]() ,∴AF=
,∴AF=![]() ﹣5=
﹣5=![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目