题目内容
已知:如图, 三点在同一条直线上,
三点在同一条直线上,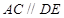 ,
,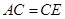 ,
,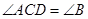 .
.求证:
 .(本题10分)
.(本题10分)
∵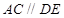 ∴
∴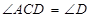 ,
,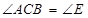
又∵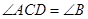 ∴
∴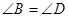 ,∵
,∵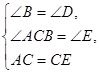 (AAS),∴
(AAS),∴ 解析:
解析:
利用AAS求证全等
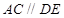 ∴
∴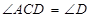 ,
,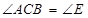
又∵
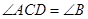 ∴
∴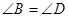 ,∵
,∵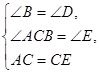 (AAS),∴
(AAS),∴ 解析:
解析:利用AAS求证全等

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
题目内容
已知:如图, 三点在同一条直线上,
三点在同一条直线上,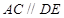 ,
,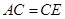 ,
,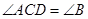 .
. .(本题10分)
.(本题10分)
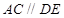 ∴
∴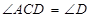 ,
,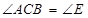
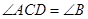 ∴
∴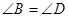 ,∵
,∵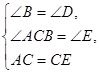 (AAS),∴
(AAS),∴ 解析:
解析:
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案