题目内容
【题目】如图，四边形ABCD内接于⊙O，AD、BC的延长线相交于点E，AB、DC的延长线相交于点F．若∠E+∠F=80°，则∠A= °．
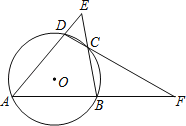
【答案】50
【解析】
试题分析：连结EF，如图，根据圆内接四边形的性质得∠A+∠BCD=180°，根据对顶角相等得∠BCD=∠ECF，则∠A+∠ECF=180°，根据三角形内角和定理得∠ECF+∠1+∠2=180°，所以∠1+∠2=∠A，再利用三角形内角和定理得到∠A+∠AEB+∠1+∠2+∠AFD=180°，则∠A+80°+∠A=180°，然后解方程即可．
解：连结EF，如图，
∵四边形ABCD内接于⊙O，
∴∠A+∠BCD=180°，
而∠BCD=∠ECF，
∴∠A+∠ECF=180°，
∵∠ECF+∠1+∠2=180°，
∴∠1+∠2=∠A，
∵∠A+∠AEF+∠AFE=180°，
即∠A+∠AEB+∠1+∠2+∠AFD=180°，
∴∠A+80°+∠A=180°，
∴∠A=50°．
故答案为：50．
一本好题口算题卡系列答案【题目】一次安全知识测验中，学生得分均为整数，满分10分，这次测验中甲、乙两组学生人数都为6人，成绩如下（单位：分）：
甲：7，9，10，8，5，9；
乙：9，6，8，10，7，8
（1）请补充完整下面的成绩统计分析表：
平均分 | 方差 | 众数 | 中位数 | |
甲组 | 8 |
| 9 |
|
乙组 |
|
| 8 | 8 |
（2）甲组学生说他们的众数高于乙组，所以他们的成绩好于乙组，但乙组学生不同意甲组学生的说法，认为他们组的成绩要好于甲组，请你给出一条支持乙组学生观点的理由． ．
【题目】学习完一次函数后，小荣遇到过这样的一个新颖的函数：y=|x﹣1|，小荣根据学校函数的经验，对函数y=|x﹣1|的图象与性质进行了探究．下面是小荣的探究过程，请补充完成：
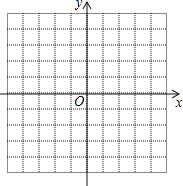
（1）列表：下表是y与x的几组对应值，请补充完整．
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 4 | 2 | 1 | … |
（2）描点连线：在平面直角坐标系xOy中，请描出以上表中各对对应值为坐标的点，画出该函数的图象；
（3）进一步探究发现，该函数图象的最低点的坐标是（1，0），结合函数的图象，写出该函数的其他性质（一条即可）： ．
