题目内容
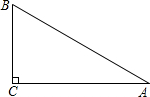
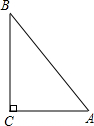
在△ABC中，∠C=90°，∠A的平分线AD交BC于D，则
等于（ ）
| CD |
| (AB-AC) |
| A．sinBAC | B．cosBAC | C．tgBAC | D．ctgBAC |
过D作DE⊥AB于E，
∵AD是∠BAC的平分线，∴DE=CD，
∵AD=AD，∠AED=∠C=90°，
∴Rt△AED≌Rt△ACD，∴AE=AC，
∴
=
=
=cot∠BDE，
∵△ABC是直角三角形，△BDE是直角三角形，
∴∠B+∠BDE=90°，∠B+∠BAC=90°，
∴∠BDE=∠BAC，
∴cot∠BDE=cot∠BAC=
．
故选D．
∵AD是∠BAC的平分线，∴DE=CD，
∵AD=AD，∠AED=∠C=90°，
∴Rt△AED≌Rt△ACD，∴AE=AC，
∴
| CD |
| (AB-AC) |
| DE |
| AB-AE |
| DE |
| BE |
∵△ABC是直角三角形，△BDE是直角三角形，
∴∠B+∠BDE=90°，∠B+∠BAC=90°，
∴∠BDE=∠BAC，
∴cot∠BDE=cot∠BAC=
| CD |
| (AB-AC) |
故选D．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
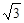取1.732）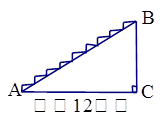
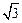，D为CB延长线上一点，且BD=2AB．求AD的长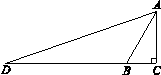
的速度向B移动，到达B后停止；t（秒）为E点移动的时间．
