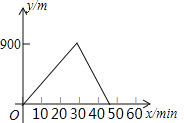
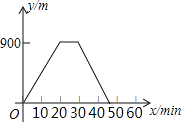
题目内容
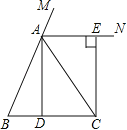
【题目】已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.
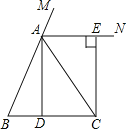
【答案】证明见解析.
【解析】试题分析:根据AN是△ABC外角∠CAM的平分线,推得∠MAE=(∠B+∠ACB),再由∠B=∠ACB,得∠MAE=∠B,则AN∥BC,根据CE⊥AN,得出四边形ADCE为矩形.
证明:∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠MAC,
∵∠MAC=∠B+∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠MAE=∠B,
∴AN∥BC,
∵AB=AC,点D为BC中点,
∴AD⊥BC,
∵CE⊥AN,
∴AD∥CE,
∴四边形ADCE为平行四边形(有两组对边分别平行的四边形是平行四边形),
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形(有一个角是直角的平行四边形是矩形).

练习册系列答案
相关题目