题目内容
【题目】定义：有一组邻边均和一条对角线相等的四边形叫做邻和四边形．
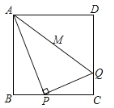
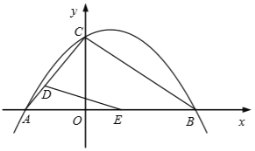
（1）如图1，四边形ABCD中，∠ABC＝70°，∠BAC＝40°，∠ACD＝∠ADC＝80°，求证：四边形ABCD是邻和四边形．
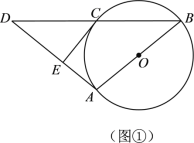
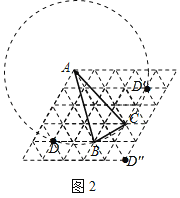
（2）如图2，是由50个小正三角形组成的网格，每个小正三角形的顶点称为格点，已知A，B，C三点的位置如图，请在网格图中标出所有的格点D，使得以A，B，C，D为顶点的四边形为邻和四边形．
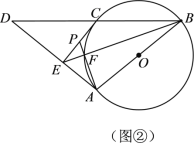
（3）如图3，△ABC中，∠ABC＝90°，AB＝4，BC＝4
，若存在一点D，使四边形ABCD是邻和四边形，求邻和四边形ABCD的面积．
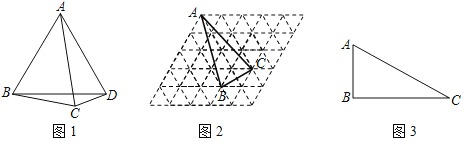
【答案】（1）详见解析；（2）详见解析；（3）24
或16．
【解析】
（1）根据题意先由三角形的内角和为180°求得∠ACB的度数，从而根据等腰三角形的判定证得AB＝AC＝AD，按照邻和四边形的定义即可得出结论；
（2）根据题意以点A为圆心，AB长为半径画圆，与网格的交点，以及△ABC外侧与点B和点C组成等边三角形的网格点即为所求；
（3）由题意先根据勾股定理求得AC的长，再分类计算即可：①当DA＝DC＝AC时；②当CD＝CB＝BD时；③当DA＝DC＝DB或AB＝AD＝BD时．
解：（1）∵∠ACB＝180°﹣∠ABC﹣∠BAC＝70°，
∴∠ACB＝∠ABC，
∴AB＝AC．
∵∠ACD＝∠ADC，
∴AC＝AD，
∴AB＝AC＝AD．
∴四边形ABCD是邻和四边形．
（2）如图，格点D，D'，D'即为所求作的点．
（3）∵在△ABC中，∠ABC＝90°，AB＝4，BC＝4，
∴AC＝
＝8，
显然AB，BC，AC互不相等．分两种情况讨论：
①当DA＝DC＝AC时，如图所示：
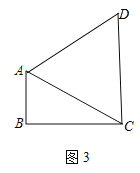
∴S△ADC＝
AC2＝16，S△ABC＝
AB×BC＝8．
∴S四边形ABCD＝S△ADC+S△ABC＝24；
②当CD＝CB＝BD时，如图所示：
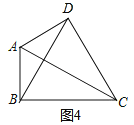
∴S△BDC＝BC2＝12，S△ADB＝AB（span>BC）＝4，
∴S四边形ABCD＝S△BDC+S△ADB＝16；
③当DA＝DC＝DB或AB＝AD＝BD时，邻和四边形ABCD不存在．
∴邻和四边形ABCD的面积是24或16．
