题目内容
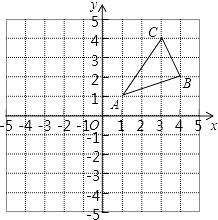
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4) 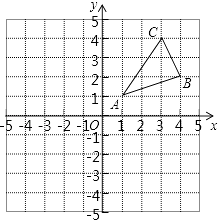 .
.
(1)请画出△ABC关于原点对称的△A2B2C2;并写出各点的坐标.
(2)在x轴上求作一点P,使△PAB的周小最小,请画出△PAB,并直接写出P的坐标.
【答案】
(1)解:△A2B2C2如图所示:
坐标为:A2(﹣1,﹣1),B2(﹣4,﹣2),C2(﹣3,﹣4)

(2)解:作出点A关于x轴的对称点A′,连接A′B与x轴相交于点P,
连接AP、BP,
即可得出△PAB,
点P坐标为(2,0)
【解析】(1)分别作出点A、B、C关于原点对称的点,然后顺次连接,并写出坐标;(2)找出点A关于x轴的对称点A′,连接A′B与x轴相交于一点,根据轴对称确定最短路线问题,交点即为所求的点P的位置,然后连接AP、BP并根据图象写出点P的坐标即可.
【考点精析】认真审题,首先需要了解轴对称-最短路线问题(已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径).

练习册系列答案
相关题目