题目内容
【题目】阅读下列材料,学习完“代入消元法”和“加减消元法“解二元一次方程组后,善于思考的小铭在解方程组![]() 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
解:将方程②变形:4x+10y+y=5,即2(2x+5y)+y=5③.
把方程①代入③得:2×3+y=5,∴y=﹣1①得x=4,所以,方程组的解为![]() .
.
请你解决以下问题:
(1)模仿小铭的“整体代换”法解方程组![]() .
.
(2)已知x,y满足方程组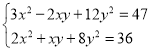 ,求x2+4y2﹣xy的值.
,求x2+4y2﹣xy的值.
【答案】(1)![]() ;(2)15
;(2)15
【解析】
(1)把9x﹣4y=19变形为3x+2(3x﹣2y)=19,再用整体代换的方法解题;
(2)将原方程组变形为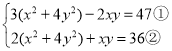 这样的形式,再利用整体代换的方法解决.
这样的形式,再利用整体代换的方法解决.
解:(1)解方程组
把②变形为3x+2(3x﹣2y)=19,
∵3x﹣2y=5,
∴3x+10=19,
∴x=3,
把x=3代入3x﹣2y=5得y=2,
即方程组的解为![]() ;
;
(2)原方程组变形为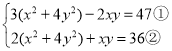
①+②×2得,7(x2+4y2)=119,
∴x2+4y2=17,
把x2+4y2=17代入②得xy=2
∴x2+4y2﹣xy=17﹣2=15
答:x2+4y2﹣xy的值是15.

练习册系列答案
相关题目



