题目内容
【题目】已知an＋1·am＋n＝a6，且m＝2n＋1，求mn的值．
【答案】3
【解析】试题分析：根据同底数幂的乘法法则可得am＋2n＋1＝a6，即可得m＋2n＋1＝6，把m＝2n＋1代入求得m的值，再求n的值即可求得mn的值．
试题解析：
由an＋1·am＋n＝a6得am＋2n＋1＝a6，即m＋2n＋1＝6，
又因为m＝2n＋1，所以2m＝6，得m＝3，则n＝1,
所以mn=3.
练习册系列答案
相关题目
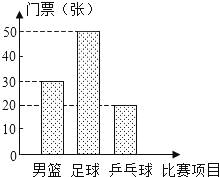
【题目】下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格，某公司购买的门票种类、数量绘制的条形统计图如图．
比赛项目 | 票价（元/张） |
男 篮 | 1000 |
足 球 | 800 |
乒乓球 | x |
依据上列图、表，回答下列问题：
（1）其中观看男篮比赛的门票有 张；观看乒乓球比赛的门票占全部门票的 %；
（2）公司决定采用随机抽取的方式把门票分配给100名员工，在看不到门票的条件下，每人抽取一张（假设所有的门票形状、大小、质地等完全相同且充分洗匀），问员工小亮抽到足球门票的概率是 ；
（3）若购买乒乓球门票的总款数占全部门票总款数的
，试求每张乒乓球门票的价格．
