题目内容
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(3)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
【答案】
(1)解:把点A(4,0),B(1,3)代入抛物线y=ax2+bx得 ![]() ,解得
,解得 ![]() ,
,
∴抛物线表达式为:y=﹣x2+4x;
(2)解:过P点作PD⊥BH交BH于点D,如图1, 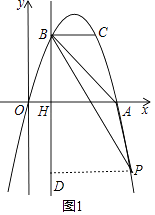
设点P(m,﹣m2+4m),
BH=AH=3,HD=m2﹣4m,PD=m﹣1,
∵S△ABP=S△ABH+S四边形HAPD﹣S△BPD,
![]() ×3×3+
×3×3+ ![]() (3+m﹣1)(m2﹣4m)﹣
(3+m﹣1)(m2﹣4m)﹣ ![]() (m﹣1)(3+m2﹣4m)=6,
(m﹣1)(3+m2﹣4m)=6,
整理得3m2﹣15m=0,解得m1=0(舍去),m2=5,
∴点P坐标为(5,﹣5);
(3)解:∵抛物线的对称性为直线x=2,
而点C、B关于抛物线的对称轴对称,
∴C(3,3),
以点C、M、N为顶点的三角形为等腰直角三角形时,分三类情况讨论:
①以点M为直角顶点且M在x轴上方时,如图2, 
CM=MN,∠CMN=90°,易证得△CBM≌△MHN,
∴BC=MH=2,BM=HN=3﹣2=1,
∴MC= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
②以点M为直角顶点且M在x轴下方时,如图3, 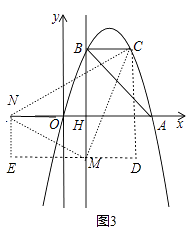
过点M作DE⊥y轴,作NE⊥DE于E,CD⊥DE于D,作辅助线,易得Rt△NEM≌Rt△MDC,
∴MD=NE=BC=2,EM=CD=BM=3+2=5,
∴CM= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
③以点N为直角顶点且N在y轴左侧时,如图4, 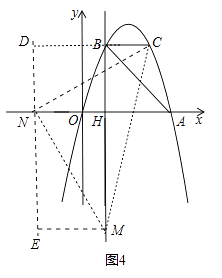
CN=MN,∠MNC=90°,易得Rt△NEM≌Rt△CDN,
∴EM=DN=BH=3,NE=CD=BD+BC=EM+BC=5,
∴CN= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =17;
=17;
④以点N为直角顶点且N在y轴右侧时,如图5, 
易得Rt△NEM≌Rt△CDN,
∴EM=DN=BH=3,NE=CD=BD﹣BC=EM﹣BC=1,
∴CN= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =5;
=5;
⑤以C为直角顶点时,不能构成满足条件的等腰直角三角形;
综上所述:△CMN的面积为: ![]() 或
或 ![]() 或17或5.
或17或5.
【解析】本题是二次函数与几何的综合题目.此题目综合性比较强,解答此题的关键是结合图形做出辅助线.
(1)利用待定系数法求出抛物线的表达式;
(2)过P作PD⊥BH交BH于点D,设P点的坐标为![]() ,则BH=AH=3,HD=m2-4m,PD=m-1,根据S△ABP+S四边形HAPD-S△BPD得到关于m的方程,解方程可得P的坐标;
,则BH=AH=3,HD=m2-4m,PD=m-1,根据S△ABP+S四边形HAPD-S△BPD得到关于m的方程,解方程可得P的坐标;
(3)先利用抛物线的对称性得到C(3,3),下面分五种情况讨论:①以点M在直角顶点且M在x轴上方时;②以点M在直角顶点且M在x轴下方时;③以点N在直角顶点且N在y轴左侧时;④以点N在直角顶点且N在y轴右侧时;⑤以点C在直角顶点时,不能构成满足条件的等腰直角三角形.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】一辆汽车在公路上行驶,其所走的路程和所用的时间可用下表表示:
时间t(min) | 1 | 2.5 | 5 | 10 | 20 | 50 | … |
路程s(km) | 2 | 5 | 10 | 20 | 40 | 100 | … |
(1)在这个变化过程中,自变量、因变量各是什么?
(2)当汽车行驶的路程为20 km时,所花的时间是多少分钟?
(3)随着t逐渐变大,s的变化趋势是什么?
(4)路程s与时间t之间的函数表达式为______________.
(5)按照这一行驶规律,当所花的时间t是300 min时,汽车行驶的路程s是多少千米?