题目内容
 如图,?ABCD中,AC⊥CD,以C为圆心,CA为半径作圆弧交BC于E,交CD的延长线于点F,以AC上一点O为圆心OA为半径的圆与BC相切于点M,交AD于点N.若AC=9cm,OA=3cm,则图中阴影部分的面积为________cm2.
如图,?ABCD中,AC⊥CD,以C为圆心,CA为半径作圆弧交BC于E,交CD的延长线于点F,以AC上一点O为圆心OA为半径的圆与BC相切于点M,交AD于点N.若AC=9cm,OA=3cm,则图中阴影部分的面积为________cm2.
21π-
分析:阴影部分的面积=扇形ECF的面积-△ACD的面积-△OCM的面积-扇形AOM的面积-弓形AN的面积.
解答: 解:连接OM,ON.
解:连接OM,ON.
∴OM=3,OC=6,
∴∠ACM=30°,
∴CD=AB=3 ,
,
∴扇形ECF的面积= =27π;
=27π;
△ACD的面积=AC×CD÷2= ;
;
扇形AOM的面积= =3π;
=3π;
弓形AN的面积= -
- ×
× ×3
×3 =3π-
=3π-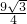 ;
;
△OCM的面积= ×3×3
×3×3 =
=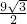 ;
;
∴阴影部分的面积=扇形ECF的面积-△ACD的面积-△OCM的面积-扇形AOM的面积-弓形AN的面积=( 21π- )cm2.
)cm2.
故答案为21π- .
.
点评:本题考查了扇形的面积的计算及平行四边形的性质,解决本题的关键是得到阴影部分的组成.

分析:阴影部分的面积=扇形ECF的面积-△ACD的面积-△OCM的面积-扇形AOM的面积-弓形AN的面积.
解答:
 解:连接OM,ON.
解:连接OM,ON.∴OM=3,OC=6,
∴∠ACM=30°,
∴CD=AB=3
 ,
,∴扇形ECF的面积=
 =27π;
=27π;△ACD的面积=AC×CD÷2=
 ;
;扇形AOM的面积=
 =3π;
=3π;弓形AN的面积=
 -
- ×
× ×3
×3 =3π-
=3π-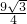 ;
;△OCM的面积=
 ×3×3
×3×3 =
=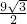 ;
;∴阴影部分的面积=扇形ECF的面积-△ACD的面积-△OCM的面积-扇形AOM的面积-弓形AN的面积=( 21π-
 )cm2.
)cm2.故答案为21π-
 .
.点评:本题考查了扇形的面积的计算及平行四边形的性质,解决本题的关键是得到阴影部分的组成.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,?ABCD中,AB⊥AC,AB=1,BC=
如图,?ABCD中,AB⊥AC,AB=1,BC=| 5 |
| A、当旋转角为90°时,四边形ABEF一定为平行四边形 |
| B、在旋转的过程中,线段AF与EC总相等 |
| C、当旋转角为45°时,四边形BEDF一定为菱形 |
| D、当旋转角为45°时,四边形ABEF一定为等腰梯形 |
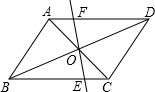
 9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )
9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )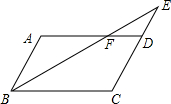 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=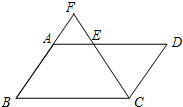 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F. (1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为
(1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为