题目内容
如图,已知线段AB、CD分别表示甲、乙两幢楼的高,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°,已知甲楼高AB=24m,求乙楼CD的高.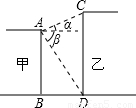
【答案】分析:首先过A作AE⊥CD于E,由AB⊥BD,CD⊥BD,可得四边形ABDE是矩形,则可求得DE的长,然后由三角函数的性质,求得CE的长,即可求得答案.
解答: 解:如图,过A作AE⊥CD于E,
解:如图,过A作AE⊥CD于E,
∵AB⊥BD,CD⊥BD,
∴四边形ABDE是矩形,
∴DE=AB=24m,
∵在Rt△AED中,AE=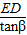 =
=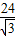 =8
=8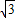 (m),
(m),
∴在Rt△ACE中,CE=AE•tanα=8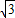 ×
×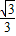 =8(m),
=8(m),
∴CD=DE+CE=24+8=32(m).
答:乙楼CD的高为32m.
点评:此题考查了仰角与俯角的知识.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.
解答:
 解:如图,过A作AE⊥CD于E,
解:如图,过A作AE⊥CD于E,∵AB⊥BD,CD⊥BD,
∴四边形ABDE是矩形,
∴DE=AB=24m,
∵在Rt△AED中,AE=
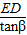 =
=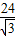 =8
=8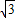 (m),
(m),∴在Rt△ACE中,CE=AE•tanα=8
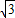 ×
×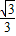 =8(m),
=8(m),∴CD=DE+CE=24+8=32(m).
答:乙楼CD的高为32m.
点评:此题考查了仰角与俯角的知识.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
如图,已知线段AB=10cm,点C是AB上任一点,点M、N分别是AC和CB的中点,则MN的长度为( )


| A、6cm | B、5cm | C、4cm | D、3cm |
 如图,已知线段AB,延长AB至C,使得BC=
如图,已知线段AB,延长AB至C,使得BC=| 1 |
| 2 |
| A、4cm | B、8cm |
| C、10cm | D、12cm |


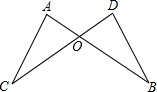 如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.
如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.