题目内容
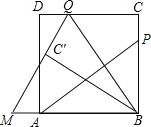
【题目】如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
【答案】(1)证明略 ;(2)![]()
【解析】
(1)要证AP=BQ,只需证△PBA≌△QCB即可;
(2)过点Q作QH⊥AB于H,如图.易得QH=BC=AB=3,BP=2,PC=1,然后运用勾股定理可求得AP(即BQ)=![]() ,BH=2.易得DC∥AB,从而有∠CQB=∠QBA.由折叠可得∠C′QB=∠CQB,即可得到∠QBA=∠C′QB,即可得到MQ=MB.设QM=x,则有MB=x,MH=x-2.在Rt△MHQ中运用勾股定理就可解决问题;
,BH=2.易得DC∥AB,从而有∠CQB=∠QBA.由折叠可得∠C′QB=∠CQB,即可得到∠QBA=∠C′QB,即可得到MQ=MB.设QM=x,则有MB=x,MH=x-2.在Rt△MHQ中运用勾股定理就可解决问题;
解:(1)AP=BQ.
理由:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∴∠ABQ+∠CBQ=90°.
∵BQ⊥AP,
∴∠PAB+∠QBA=90°,
∴∠PAB=∠CBQ.
在△PBA和△QCB中,
 ,
,
∴△PBA≌△QCB,
∴AP=BQ;
(2)过点Q作QH⊥AB于H,如图.
∵四边形ABCD是正方形,
∴QH=BC=AB=3.
∵BP=2PC,
∴BP=2,PC=1,
∴BQ=AP=![]() =
=![]() =
=![]() ,
,
∴BH=![]() =
=![]() =2.
=2.
∵四边形ABCD是正方形,
∴DC∥AB,
∴∠CQB=∠QBA.
由折叠可得∠C′QB=∠CQB,
∴∠QBA=∠C′QB,
∴MQ=MB.
设QM=x,则有MB=x,MH=x-2.
在Rt△MHQ中,
根据勾股定理可得x2=(x-2)2+32,
解得x=![]() .
.
∴QM的长为![]() ;
;


练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目