Question

【题目】某景区的三个景点在同一线路上，甲、乙两名游客从景点出发，甲步行到景点乙乘景区观光车先到景点在处停留一段时间后，再步行到景点．甲、乙两人离开景点后的路程(米)关于时间(分钟)的函数图象如图所示．根据以上信息回答下列问题：

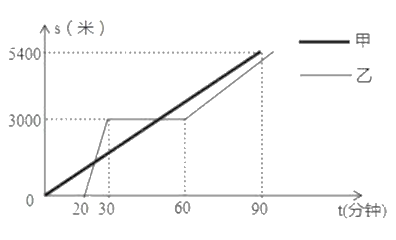
（1）乙出发后多长时间与甲相遇?

（2）若当甲到达景点时，乙与景点的路程为米，则乙从景点步行到景点的速度是多少?

Answer 1

【答案】（1）乙出发5分钟或30分钟后与甲相遇；（2）乙步行由到的速度为米/分钟

【解析】

（1）根据图象确定出甲步行路程与时间的解析式；确定出20≤t≤30时，乙乘观光车由景点A到B时的路程与时间的函数解析式，联立即可确定出相遇的时间；
（2）设当60≤t≤90时，乙步行由景点B到C的速度为x米/分钟，根据题意列出方程，求出方程的解得到x的值，即可确定出乙步行由B到C的速度．

解:当时，甲步行路程与时间的函数解析式为;

当20≤t≤30时，设乙乘观光车由景点到时的路程与时间的函数解析式为,

把与代入

得

解得

∴函数解析式为S=300t-6000（20≤t≤30）；
联立得： ，
解得： ，

乙出发分钟后与甲相遇；

由60t=3000，得到t=50，即50-20=30，
则乙出发5分钟或30分钟后与甲相遇；

设当时，乙步行由景点到的速度为米/分钟，

根据题意，得

解得：

乙步行由到的速度为米/分钟.