��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���![]() Ϊ���Σ���
������![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ٶ���
����λ���ٶ���![]() ���յ�
���յ�![]() �˶�������
�˶�������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��������
��������![]() �˶���
�˶���![]() ��ʱ��
��ʱ��
��1��![]() �������Ϊ________��
�������Ϊ________��![]() �������Ϊ________���ú�
�������Ϊ________���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ
�ĺ�����ϵʽ![]() ���������
���������![]() ȡ��ֵʱ��
ȡ��ֵʱ��![]() �����ֵ�����ֵ�Ƕ��٣�
�����ֵ�����ֵ�Ƕ��٣�
��2����![]() ������ͬʱ����һ����
������ͬʱ����һ����![]() ��
��![]() �㿪ʼ���߶�
�㿪ʼ���߶�![]() ����ÿ��
����ÿ��![]() ����λ���ȵ��ٶ����
����λ���ȵ��ٶ����![]() �ƶ�������
�ƶ�������![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��![]() ���ƣ�
���ƣ�

���𰸡�(1)![]() ��
��![]() ;(2)3;(3)
;(2)3;(3)![]() ��
��![]() .
.
��������
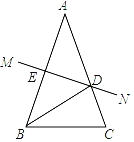
��1������ؼ�����N�����꣬����N������Ҳ�������P�����꣬���Dz��ѷ���M��N����ԭ��Գƣ����ֻҪ���M������������N�����꣬���ǿ�M�����꣬����֪��M���ٶȣ�������ʱ��t��ʾ��BM�ij�����ôOB-BMsin��BAC����M�������꣬BMsin��ABP����M�ĺ����꣬��BAC�͡�ABP������ֵ�����ڡ�AOB�������˾������M��N��P�������ˣ���2������NP������MNP�ĵױߣ���ô���ij��Ⱦ���N�������ľ���ֵ����NP���ϵĸ߾���M��P������IJ�ľ���ֵ����˿ɸ��������ε������ʽ�ó�����S��t�ĺ�����ϵʽ����3��Ҫ��������ۣ���Ϊ���������ι����ˡ�BAO���ֻҪ��������ġ�MQA��������������ĸ���ֱ�ǾͿ����ˣ��ɸ������������Ƶó��߶εı�������⣮
��1��![]()
��2��![]() ��
��
![]() ʱ��
ʱ��![]() �����ֵ��
�����ֵ��![]() ��
��
��3��![]() ��
��![]() ���ƣ���������ۣ�
���ƣ���������ۣ�
��![]() ʱ����
ʱ����![]() ��
��![]() �ĺ�������ȣ�
�ĺ�������ȣ�
![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ʱ����
ʱ����![]() �ɵã�
�ɵã�
![]() ��
��![]() ��
��![]()
����Ϊ![]() ��������ֱ�ǣ�����������������ڣ�
��������ֱ�ǣ�����������������ڣ�
����![]() Ϊ
Ϊ![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() ���ƣ�
���ƣ�

����Ŀ��ijѧУ������У������У�ͱ�У��������У�����꼶ѧ������300����Ϊ�˽�������У�����꼶ѧ����Ӣ�ﵥ����������������˳������飬�������£�
���ռ����ݣ�����У�ͱ�У����У���ľ��꼶�������ȡ10��ѧ��������Ӣ�ﵥ�ʲ��ԣ����Գɼ����ٷ��ƣ����£�
��У 92 100 86 89 73 98 54 95 98 85
��У 100 100 94 83 74 86 75 100 73 75
���������������ݣ������·����������������������������ݣ�
�ɼ�x ���� ���� | ��50��x��59 | 60��x��69 | 70��x��79 | 80��x��89 | 90��x��100 |
����У | ��1 | ��0 | 1 | 3 | 5 |
����У | ��0 | ��0 | ��4 | 2 | 4 |
��˵�����ɼ�90�ּ�����Ϊ���㣬80��89�ַ�Ϊ���ã�60��79��Ϊ�ϸ�60������Ϊ���ϸ�
�۷������ݣ����������ݽ��з������ֱ�����������������ݵ�ƽ��������λ�����������������±���
У�� | ƽ���� | ��λ�� | ���� | ���� |
��У | 87 | 90.5 | �� ���� | 179.4 |
��У | 86 | �� �� | �� �� | 121.6 |
�ܵó����ۣ�
�������ͳ��ȫ���̣��ش��������⣺
��1����ȫ���еı���
��2������Ʊ�У���꼶ѧ��Ӣ�ﵥ�����������������
��3������Ϊ�ĸ�У���ľ��꼶ѧ��Ӣ�ﵥ�����յñȽϺã�˵��������ɣ������ٴ�������ͬ�ĽǶ�˵���ƶϵĺ����ԣ�