题目内容
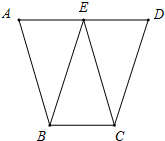在四边形ABCD中，AD∥BC，且AD=2BC，取AD的中点E，并连接BE，CE．请找出图形中的平行四边形，并说明理由．
解：平行四边形为：四边形ABCE和四边形DCBE，理由是：
∵AD=2BC，E为AD的中点，
∴AE=ED=BC，
∵AD∥BC，
∴四边形ABCE和四边形DCBE都是平行四边形．
分析：推出AE=ED=BC，根据有一组对边相等且平行的四边形是平行四边形推出即可．
点评：本题考查了对平行四边形的判定定理的应用，本题用到了平行四边形的判定定理：有一组对边相等且平行的四边形是平行四边形．
∵AD=2BC，E为AD的中点，
∴AE=ED=BC，
∵AD∥BC，
∴四边形ABCE和四边形DCBE都是平行四边形．
分析：推出AE=ED=BC，根据有一组对边相等且平行的四边形是平行四边形推出即可．
点评：本题考查了对平行四边形的判定定理的应用，本题用到了平行四边形的判定定理：有一组对边相等且平行的四边形是平行四边形．
练习册系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
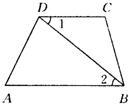11、如图所示，在四边形ABCD中，BD是它的一条对角线，若∠1=∠2，∠A=55°16′，则∠ADC=
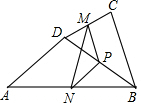如图，在四边形ABCD中，AD=BC，P是对角线BD的中点，M是边DC的中点，N是边AB的中点．△MPN是什么三角形？为什么？