题目内容
如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连结AB、PB、AC,BP分别与AD、AC相交于点E、F.
(1)BE与EF相等吗?并说明理由;
(2)小李通过操作发现CF=2AB,请问小李的发现是否正确,若正确,请说明理由;若不正确,请写出CF与AB正确的关系式.
(3)求 的值.
的值.
(1)相等,理由见解析;(2)正确;(3)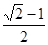 .
.
解析试题分析:(1)根据圆周角定理求出∠ABE=∠BAE,求出AE=BE,求出∠CAD=∠AFB,求出AE=EF,即可得出答案;
(2)根据全等三角形的性质和判定求出BG=CF,AB=AG,即可得出答案;
(3)求出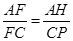 ,求出AH、CP的长,代入即可求出答案.
,求出AH、CP的长,代入即可求出答案.
试题解析:(1)BE=EF,
理由是:∵BC是直径,AD⊥BC,
∴∠BAC=∠ADC=90°,
∴∠BAD=∠ACB,
∵A为弧BP中点,
∴∠ABP=∠ACB,
∴∠BAD=∠ABP,
∴BE=AE,∠FAD=∠AFB,
∴EF=AE,
∴BE=EF;
(2)小李的发现是正确的,
理由是:延长BA、CP,两线交于G,
∵P为半圆弧的中点,A是弧BP的中点,
∴∠PCF=∠GBP,∠CPF=∠BPG=90°,BP=PC,
在△PCF和△PBG中,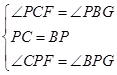
∴△PCF≌△PBG(ASA),
∴CF=BG,
∵BC为直径,
∴∠BAC=°,
∵A为弧BP中点,
∴∠GCA=∠BCA,
在△BAC和△GAC中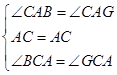
∴△BAC≌△GAC(ASA),
∴AG=AB= BG,
BG,
∴CF=2AB;
(3)连接OA交BP于H,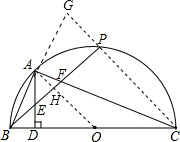
∵A为弧BP的中点,
∴OA⊥BP,
∵∠BPC=90°,
∴OA∥CP,
∴△AHF∽△CPF,
∴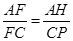 ,
,
设OA=r,BC=2r,
∵BP=CP,∠BPC=90°,
∴PC=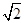 r,
r,
∴OH=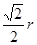 ,AH=
,AH=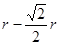 ,
,
∴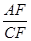 =
=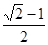 .
.
考点:1.相似三角形的判定与性质;2.全等三角形的判定与性质;3.圆周角定理.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 ∥
∥ ,
,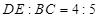 ,则
,则 .
.
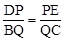

 =DM·EN
=DM·EN
 ,试画出示意图,并求出
,试画出示意图,并求出 所有可能的值;
所有可能的值;
 ,DE=2,求AD的长.
,DE=2,求AD的长.

 .
.
 ,在同一时刻测得小丽和建筑物
,在同一时刻测得小丽和建筑物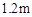 和
和 ,求建筑物
,求建筑物