题目内容
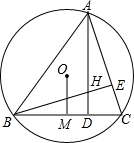
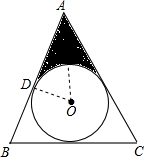
如图,∠A=60°,AB=AC=2,⊙O为△ABC的内切圆,则阴影部分的面积为______.
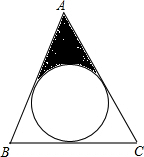

连接OA,OD(AB上的内切点).
∵∠A=60°,AB=AC=2,
∴△ABC是等边三角形,
由于等边三角形的内心就是它的外心,
可得AD=
AB=1,∠OAB=
∠CAB=30°;
在Rt△OAD中,tan30°=
,即
=
,
得0D=
.
故图中阴影部分的面积为:
(S△ABC-S⊙O)=
[(
×22-π(
)2]=
-
π.
故答案为:
-
π.
∵∠A=60°,AB=AC=2,
∴△ABC是等边三角形,
由于等边三角形的内心就是它的外心,
可得AD=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OAD中,tan30°=
| OD |
| AD |
| ||
| 3 |
| OD |
| 1 |
得0D=
| ||
| 3 |
故图中阴影部分的面积为:
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
| ||
| 3 |
| 1 |
| 9 |
故答案为:
| ||
| 3 |
| 1 |
| 9 |


练习册系列答案
相关题目
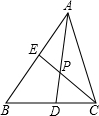

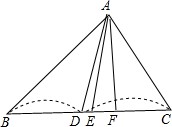 的线段在△ABC中有几条?
的线段在△ABC中有几条?