题目内容
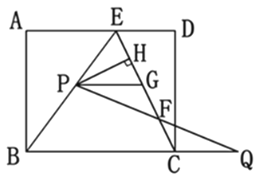
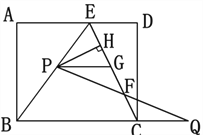
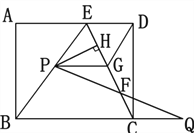
【题目】如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.
(1)求证:△PFG≌△QFC
(2)连结DG.当x为何值时,四边形PGDE是菱形,请说明理由;
(3)作PH⊥EC于点H.探究:
①点P在运动过程中,线段HF的长度是否发生变化?若变化,说明理由;若不变,求HF的长度;
②当x为何值时,△PHF与△BAE相似
【答案】(1)证明见解析;(2)当x=4时,四边形PGDE是菱形,理由见解析;(3)①不变化,HF![]() ,②当
,②当![]() 或
或![]() 时,△PHF与△BAE相似
时,△PHF与△BAE相似
【解析】试题分析:(1)根据全等三角形的判定ASA即可证出;(2)先证出PG∥BQ,AD∥BC得到四边形PGDE是平行四边形,再根据四边形PGDE是菱形得出PG=PE=4;(3)① 证出△PFG≌△QFC,求出HF的长;②分两种情况讨论得出.
试题解析:
(1)证明:∵BC=BE ∴∠BCE=∠PEC
∵PG∥BQ
∴∠BCE=∠PGE, ∠Q=∠FPG ,∠QCF=∠PGF
∴∠PGE=∠PEC
∴PE=PG
∵PE=CQ
∴ PG =CQ
∴△PFG≌△QFC (ASA)
(2)连结DG.当x=4时,四边形PGDE是菱形,
理由如下;
∵四边形ABCD是矩形,
∴AD∥BC
AB=CD=8,AD=BC=BE=10
在Rt△ABE中
AE=![]()
∴DE=AD-AE=10-6=4
由(1)知PG=PE=x=4
∴PG=DE
∵PG∥BQ,AD∥BC
∴PG∥DE
∴四边形PGDE是平行四边形,
∵PG=PE=4
∴四边形PGDE是菱形
(3)①不变化
在Rt△ABE中
CE=![]()
∵PG=PE,PH⊥EC
∴EH=HG=![]() EG(等腰三角形“三线合一”)
EG(等腰三角形“三线合一”)
∵△PFG≌△QFC
∴CF=GF=![]() CG
CG
∴HF=HG+FG=![]() EG+
EG+![]() CG=
CG=![]() CE=
CE=![]()
②∵PG∥DE, ∴∠DEC=∠PGH
在Rt△PGH中
PH=PG×sin∠PGH= x×sin∠DEC= x×![]() = x×
= x×![]() =
=![]()
分两种情况讨论:
(I)若△PHF/span>∽△EAB,则![]()
∴
∴![]()
∴当![]() 时,△PHF∽△BAE.
时,△PHF∽△BAE.
(II)若△PHF∽△BAE,则![]()
∴
∴![]()
∴当![]() 或
或![]() 时,△PHF与△BAE相似
时,△PHF与△BAE相似

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】温度通常有两种表示方法:华氏度(单位:℉)与摄氏度(单位:℃),已知华氏度数y与摄氏度数x之间是一次函数关系,如表列出了部分华氏度与摄氏度之间的对应关系:
摄氏度数x(℃) | … | 0 | … | 35 | … | 100 | … |
华氏度数y(℉) | … | 32 | … | 95 | … | 212 | … |
(1)选用表格中给出的数据,求y关于x的函数解析式(不需要写出该函数的定义域);
(2)已知某天的最低气温是﹣5℃,求与之对应的华氏度数.
