题目内容
如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为1cm2，则该半圆的直径为____▲______。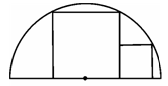
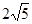cm设大正方形边长为x，根据勾股定理可得大圆半径，连接圆心和小正方形右上顶点，也可得直角三角形．
已知小正方形的面积即可求得边长，在直角△ACE中，利用勾股定理即可求解．
解：如图，圆心为A，设大正方形的边长为2x，圆的半径为R，
则AE=BC=x，CE=2x；
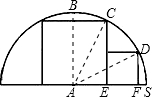
∵小正方形的面积为1cm2，
∴小正方形的边长EF=DF=1，
由勾股定理得，R2=AE2+CE2=AF2+DF2，即x2+4x2=（x+1）2+12，
解得，x=1，x=-1/2（舍去）
∴R=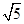
cm．
该半圆的直径为2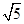cm．
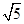故答案为：2cm．
已知小正方形的面积即可求得边长，在直角△ACE中，利用勾股定理即可求解．
解：如图，圆心为A，设大正方形的边长为2x，圆的半径为R，
则AE=BC=x，CE=2x；
∵小正方形的面积为1cm2，
∴小正方形的边长EF=DF=1，
由勾股定理得，R2=AE2+CE2=AF2+DF2，即x2+4x2=（x+1）2+12，
解得，x=1，x=-1/2（舍去）
∴R=
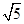cm．该半圆的直径为2
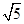cm．故答案为：2
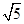cm．
练习册系列答案
同步练习强化拓展系列答案
相关题目
中，
，
，点
从
开始沿折线A-B-C-D以4cm/s的速度移动，点
从
开始沿
边以1cm/s的速度移动，如果点
时，另一点也随之停止运动。设运动时间为t(s)。
为矩形？
和
的半径都是2cm，那么t为何值时，
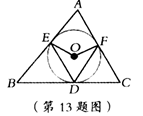
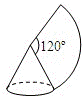
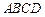是平行四边形，以AB为直径的⊙O经过点D，点E是⊙O上一点，且∠AED=45°。
，
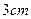，求∠ADE的正弦值．
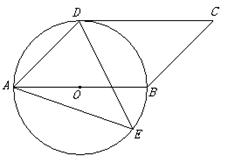
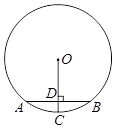
2，BC=2，以BC为直径的半圆交AB于点D，以A为圆心，AC为半径的扇形交AB于点E．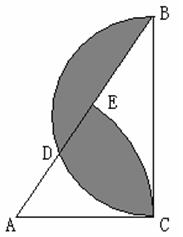
）．
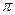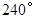的扇形铁皮，卷成一个圆锥容器的侧面（接缝忽略不计），则这个圆锥容器的底面半径是________cm.