Question

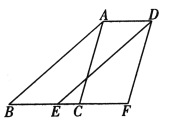
【题目】△ABC中，AB＝AC，∠ABC＝α，过点A作直线MN，使MN∥BC，点D在直线MN上，作射线BD，将射线BD绕点B顺时针旋转角α后交直线AC于点E．

（1）如图①，当α＝60°，且点D在射线AN上时，直接写出线段AB，AD，AE的数量关系．

（2）如图②，当α＝45°，且点D在射线AN上时，直写出线段AB、AD、AE的数量关系，并说明理由．

（3）当α＝30°时，若点D在射线AM上，∠ABE＝15°，AD＝﹣1，请直接写出线段AE的长度．

Answer 1

【答案】（1）AE＝AB+AD；（2）AE＝AB+AD，见解析；（3）线段AE的长度为﹣1或2﹣

【解析】

（1）当α＝60°时，可得△ABC是等边三角形，判定△BAD≌△BCE，即可得到AD＝CE，进而得到AE＝AC+CE＝AB+AD；

（2）当α＝45°时，可得△ABC是等腰直角三角形，判定△BAD∽△BCE，可得CE＝AD，进而得出AE＝AC+CE＝AB+AD；

（3）分两种情况：点E在线段AC上，点E在CA的延长线上，分别画出图形，依据∠ABE＝15°，AD＝﹣1，即可得到线段AE的长度．

（1）∵当α＝60°时，∠ABC＝∠DBE＝60°，

∴∠ABD＝∠CBE，

又∵AB＝AC，

∴△ABC是等边三角形，

∴AB＝CB，∠ACB＝60°，

∴∠BCE＝120°，

∵MN∥BC，

∴∠BAD＝180°﹣∠ABC＝120°，

∴∠BAD＝∠BCE，

∴△BAD≌△BCE，

∴AD＝CE，

∴AE＝AC+CE＝AB+AD；

（2）AE＝AB+AD．

理由：当α＝45°时，∠ABC＝∠DBE＝45°，

∴∠ABD＝∠CBE，

∵AB＝AC，

∴∠ABC＝∠ACB＝45°，∠BAC＝90°，

∴△ABC是等腰直角三角形，

∴BC＝AB，

∵MN∥BC，

∴∠BAD＝180°﹣∠ABC＝135°，

∵∠BCE＝180°﹣∠ACB＝135°，

∴∠BAD＝∠BCE，

∴△BAD∽△BCE，

∴＝＝，

∴CE＝AD，

∴AE＝AC+CE＝AB+AD；

（3）线段AE的长度为﹣1或2﹣．

由题可得，∠ABC＝∠DBE＝∠BAD＝30°，

分两种情况：

①如图所示，当点E在线段AC上时，

∵∠ABE＝15°＝∠ABC＝∠DBE，

∴∠ABD＝∠ABE＝15°，

在BE上截取BF＝BD，易得△ABD≌△ABF，

∴AD＝AF＝﹣1，∠ABC＝∠BAD＝∠BAF＝30°，

∴∠AFE＝∠ABF+∠BAF＝15°+30°＝45°，

又∵∠AEF＝∠CBE+∠C＝15°+30°＝45°，

∴∠AFE＝∠AEF，

∴AE＝AF＝﹣1；

②如图所示，当点E在CA的延长线上时，

过D作DF⊥AB于F，过E作EG⊥BC于G，

∵AD＝﹣1，∠DAF＝30°，

∴DF＝，AF＝，

∵∠DBF＝15°+30°＝45°，

∴∠DBF＝∠BDF，

∴BF＝DF＝，AB＝+＝1＝AC，

易得△ABC中，BC＝，

∵∠EBG＝15°+30°＝45°，

∴∠BEG＝∠EBG，

设BG＝EG＝x，则CG＝﹣x，

∵Rt△CEG中，tanC＝，即＝，

∴x＝＝EG，

∴CE＝2EG＝3﹣，

∴AE＝CE﹣AC＝3﹣﹣1＝2﹣

综上所述所，线段AE的长度为﹣1或2﹣．