Question

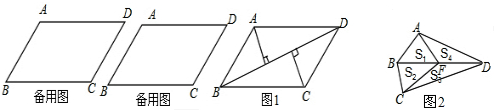
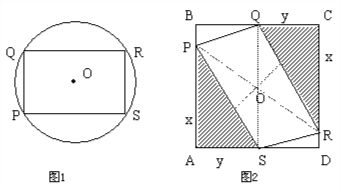
29、如图1，已知平行四边形PQRS是⊙O的内接四边形．
（1）求证：平行四边形PQRS是矩形．
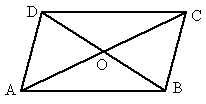
（2）如图2，如果将题目中的⊙O改为边长为a的正方形ABCD，在AB、CD上分别取点P、S，连接PS，将Rt△SAP绕正方形中心O旋转180°得Rt△QCR，从而得四边形PQRS．试判断四边形RQRS能否变化成矩形？若能，设PA=x，SA=y，请说明x、y具有什么关系时，四边形PQRS是矩形；若不能，请说明理由．

Answer 1

分析：（1）只需证明有一内角为90°即可．根据圆内接四边形对角互补及平行四边形对角相等易得结论．
（2）根据中心对称的定义易知四边形PQRS为平行四边形；若是矩形，则必有内角为直角，不妨设∠QPS=90°，此时
需满足△BPQ∽△ASP．即当BP：BQ=AS：AP时，四边形PQRS为矩形．

解答：证明：（1）∵平行四边形PQRS内接于⊙O，
∴∠Q+∠S=180°．
又∵∠Q=∠S，
∴∠Q=90°，
∴平行四边形PQRS是矩形．
（2）∵Rt△SAP与Rt△QCR关于点O对称，
∴QS与PR被O点平分，四边形PQRS为平行四边形．
若平行四边形PQRS变成矩形，不妨设∠QPS=90°．则∠BPQ+∠APS=90°．
又∵∠APS+∠ASP=90°，
∴∠BPQ=∠ASP，
∴△BPQ∽△ASP．
∴BP：BQ=AS：AP，
即 （a-x）：（a-y）=y：x，
整理得（x-y）（x+y-a）=0，
∴x=y或x+y=a．
∴当x=y或x+y=a时，
可证得△BPQ∽△ASP，此时有∠QPS=90°，
从而得平行四边形PQRS是矩形．

点评：此题考查了矩形的判定方法及相似三角形的判定和性质，为开放探索型综合题，有一定难度．此类题常用分析法求解．