题目内容
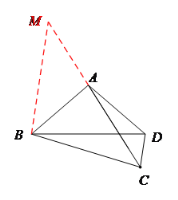
【题目】如图,四边形ABCD中,AB=AD,BC=BD,若∠ABD=![]() ∠BAC=,则∠BDC的度数为( )
∠BAC=,则∠BDC的度数为( )

A. 2B. 45°+![]() C. 90°-D. 180°-3
C. 90°-D. 180°-3
【答案】A
【解析】
作∠MBA=∠DBA,交CA延长线于M.由∠ABD=∠ADB=,∠BAC=2,得∠CAD=180°-4,易证△BAM≌△BAD,得∠M=∠ADB=,BM=BD=BC,设∠ACD=x,则∠BDC=x+,故x+(x+)=++,解得x=,故∠BDC=2
作∠MBA=∠DBA,交CA延长线于M.∠ABD=∠ADB=,∠BAC=2,
∴∠CAD=180°-4,
∴∠BAM=180°-2,∠BAD=180°-2,
∴△BAM≌△BAD,
∴∠M=∠ADB=,BM=BD=BC,
∴AB=AM,
∴∠ABM=∠M=,
∴∠ACB=∠M=,
设∠ACD=x,则∠BDC=x+,
由八字形得x+(x+)=++,
∴x=,
∴∠BDC=2

练习册系列答案
相关题目





