题目内容
(2012•潮阳区模拟)在一组数列:a1,a2,a3,…,an中,已知a1=1-
,且a2=1-
,a3=1-
,…,an=-
.
(1)求a2,a3,a4;
(2)根据以上计算过程发现的规律可求出:a2012=
(3)求a1a2a3+a2a3a4+a3a4a5+…+a2010a2011a2012.
| 1 |
| π |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an-1 |
(1)求a2,a3,a4;
(2)根据以上计算过程发现的规律可求出:a2012=
-
| 1 |
| π-1 |
-
;| 1 |
| π-1 |
(3)求a1a2a3+a2a3a4+a3a4a5+…+a2010a2011a2012.
分析:(1)将a1的值代入a2=1-
中求出a2的值,将a2的值代入a3=1-
中求出a3的值,将a3的值代入a4=-
即可求出a4的值;
(2)根据上述计算过程得到其值的规律以三个数循环,由2012除以3的余数为2,即可确定出所求的值;
(3)先计算出a1a2a3的值,根据总结得到规律发现:a1=a4=a7=…=a2011,a2=a5=a8=…=a2012,a3=a6=a9=…=a2010,进而得到a1a2a3=a2a3a4=a3a4a5=…=a2010a2011a2012=-1,即可求出所求式子的值.
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
(2)根据上述计算过程得到其值的规律以三个数循环,由2012除以3的余数为2,即可确定出所求的值;
(3)先计算出a1a2a3的值,根据总结得到规律发现:a1=a4=a7=…=a2011,a2=a5=a8=…=a2012,a3=a6=a9=…=a2010,进而得到a1a2a3=a2a3a4=a3a4a5=…=a2010a2011a2012=-1,即可求出所求式子的值.
解答:解:(1)当a1=1-
时,a2=1-
=1-
=1-
=-
,
a3=1-
=1-
=π,a4=1-
=1-
;
(2)∵2012÷3=670…2,
∴a2012=-
;
(3)由(1)得:a1a2a3=(1-
)×(-
)×π=-1;
且有一下规律:a1=a4=a7=…=a2011,a2=a5=a8=…=a2012,a3=a6=a9=…=a2010,
∴a1a2a3=a2a3a4=a3a4a5=…=a2010a2011a2012=-1,
则a1a2a3+a2a3a4+a3a4a5+…+a2010a2011a2012=-1×2010=-2010.
故答案为:(2)-
| 1 |
| π |
| 1 |
| a1 |
| 1 | ||
1-
|
| π |
| π-1 |
| 1 |
| π-1 |
a3=1-
| 1 |
| 1-a2 |
| 1 | ||
-
|
| 1 |
| a3 |
| 1 |
| π |
(2)∵2012÷3=670…2,
∴a2012=-
| 1 |
| π-1 |
(3)由(1)得:a1a2a3=(1-
| 1 |
| π |
| 1 |
| π-1 |
且有一下规律:a1=a4=a7=…=a2011,a2=a5=a8=…=a2012,a3=a6=a9=…=a2010,
∴a1a2a3=a2a3a4=a3a4a5=…=a2010a2011a2012=-1,
则a1a2a3+a2a3a4+a3a4a5+…+a2010a2011a2012=-1×2010=-2010.
故答案为:(2)-
| 1 |
| π-1 |
点评:此题考查了分式的混合运算,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时分式的分子分母出现多项式,应将多项式分解因式后再约分.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
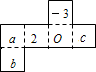 (2012•潮阳区模拟)如图是一个正方体纸盒的展开图,按虚线折成正方体后,相对面上的两个数互为相反数,则ca+b=( )
(2012•潮阳区模拟)如图是一个正方体纸盒的展开图,按虚线折成正方体后,相对面上的两个数互为相反数,则ca+b=( ) (2012•潮阳区模拟)如图是一座人行天桥的引桥部分的示意图,上桥的通道由两段互相平行楼梯AD,BE和一段水平平台DE构成.已知∠A=37°,AD=5米,DE=1.6米,BE=3米,求天桥的高度BC和引桥的水平跨度AC的长(参考数据:取sin37°=0.60,cos37°=0.80,tan37°=0.75)
(2012•潮阳区模拟)如图是一座人行天桥的引桥部分的示意图,上桥的通道由两段互相平行楼梯AD,BE和一段水平平台DE构成.已知∠A=37°,AD=5米,DE=1.6米,BE=3米,求天桥的高度BC和引桥的水平跨度AC的长(参考数据:取sin37°=0.60,cos37°=0.80,tan37°=0.75) (2012•潮阳区模拟)如图,梯形OABC,AB∥OC,∠B=90°,BC=2,底边OC与x轴重合,点D为BC的中点,且AD⊥OD.
(2012•潮阳区模拟)如图,梯形OABC,AB∥OC,∠B=90°,BC=2,底边OC与x轴重合,点D为BC的中点,且AD⊥OD.