题目内容
 (2012•潮阳区模拟)如图是一座人行天桥的引桥部分的示意图,上桥的通道由两段互相平行楼梯AD,BE和一段水平平台DE构成.已知∠A=37°,AD=5米,DE=1.6米,BE=3米,求天桥的高度BC和引桥的水平跨度AC的长(参考数据:取sin37°=0.60,cos37°=0.80,tan37°=0.75)
(2012•潮阳区模拟)如图是一座人行天桥的引桥部分的示意图,上桥的通道由两段互相平行楼梯AD,BE和一段水平平台DE构成.已知∠A=37°,AD=5米,DE=1.6米,BE=3米,求天桥的高度BC和引桥的水平跨度AC的长(参考数据:取sin37°=0.60,cos37°=0.80,tan37°=0.75)分析:首先由已知构造直角三角形如图,延长BE交AC于F,由已知BE∥AD,四边形AFED为平行四边形,所以DE=AF,再解直角三角形BCF求得CF与BC.
解答: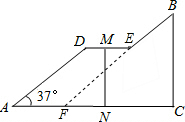 解:延长BE交AC于F,
解:延长BE交AC于F,
∵AD∥BE,∴AD∥EF,
∴∠BFC=∠A=37°,
又∵DE∥AF,
∴四边形ADEF是平行四边形,
∴DE=AF=1.6m,EF=AD=5m,
∴BF=BE+EF=3+5=8(m),
在Rt△BFC中,∵sin∠BFC=
,cos∠BFC=
,
∴BC=BFsin∠BFC=8×sin37°=8×0.6=4.8(米),
FC=BF×cos∠BFC=8×cos37°=8×0.80=6.4(m),
∴AC=AF+FC=1.6+6.4=8(m).
答:天桥的高度BC为4.8m,引桥的水平跨度AC的长为8米.
 解:延长BE交AC于F,
解:延长BE交AC于F,∵AD∥BE,∴AD∥EF,
∴∠BFC=∠A=37°,
又∵DE∥AF,
∴四边形ADEF是平行四边形,
∴DE=AF=1.6m,EF=AD=5m,
∴BF=BE+EF=3+5=8(m),
在Rt△BFC中,∵sin∠BFC=
| BC |
| BF |
| FC |
| BF |
∴BC=BFsin∠BFC=8×sin37°=8×0.6=4.8(米),
FC=BF×cos∠BFC=8×cos37°=8×0.80=6.4(m),
∴AC=AF+FC=1.6+6.4=8(m).
答:天桥的高度BC为4.8m,引桥的水平跨度AC的长为8米.
点评:此题考查了解直角三角形的应用,关键是由已知首先构建直角三角形,运用三角函数求解.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
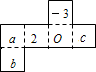 (2012•潮阳区模拟)如图是一个正方体纸盒的展开图,按虚线折成正方体后,相对面上的两个数互为相反数,则ca+b=( )
(2012•潮阳区模拟)如图是一个正方体纸盒的展开图,按虚线折成正方体后,相对面上的两个数互为相反数,则ca+b=( ) (2012•潮阳区模拟)如图,梯形OABC,AB∥OC,∠B=90°,BC=2,底边OC与x轴重合,点D为BC的中点,且AD⊥OD.
(2012•潮阳区模拟)如图,梯形OABC,AB∥OC,∠B=90°,BC=2,底边OC与x轴重合,点D为BC的中点,且AD⊥OD.