题目内容
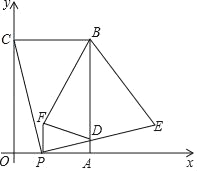
【题目】如图,![]() 中,
中,![]() ,
,![]() 的平分线
的平分线![]() 与边
与边![]() 的垂直平分线
的垂直平分线![]() 相交于点
相交于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 于点
于点![]() ,现有下列结论:①
,现有下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() ,其中正确的是( )
,其中正确的是( )

A.①②B.①②③C.①②④D.①②③④
【答案】C
【解析】
①由角平分线的性质可知①正确;
②由题意可知∠EAD=∠FAD=30°,故此可知ED=![]() AD,DF=
AD,DF=![]() AD,从而可证明②正确;
AD,从而可证明②正确;
③若DM平分∠EDF,则∠EDM=90°,从而得到∠ABC为直角三角形,条件不足,不能确定,故③错误;
④连接BD、DC,然后证明△EBD≌△DFC,从而得到BE=FC,从而可证明④.
解:如图所示:连接BD、DC.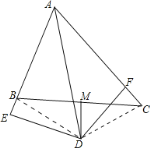
①∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴ED=DF.
∴①正确.
②∵∠EAC=60°,AD平分∠BAC,
∴∠EAD=∠FAD=30°.
∵DE⊥AB,
∴∠AED=90°.
∵∠AED=90°,∠EAD=30°,
∴ED=![]() AD.
AD.
同理:DF=![]() AD.
AD.
∴DE+DF=AD.
∴②正确.
③由题意可知:∠EDA=∠ADF=60°.
假设MD平分∠EDF,则∠ADM=30°.则∠EDM=90°,
又∵∠E=∠BMD=90°,
∴∠EBM=90°.
∴∠ABC=90°.
∵∠ABC是否等于90°不知道,
∴不能判定MD平分∠EDF,
故③错误.
④∵DM是BC的垂直平分线,
∴DB=DC.
在Rt△BED和Rt△CFD中
![]() ,
,
∴Rt△BED≌Rt△CFD.
∴BE=FC.
∴AB+AC=AE-BE+AF+FC
又∵AE=AF,BE=FC,
∴AB+AC=2AE.故④正确.
综上所述,①②④正确,
故选:C.

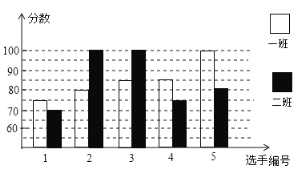
【题目】某学校八年级开展英语拼写大赛,一班和二班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表
班级 | 中位数(分) | 众数(分) | 平均数(分) |
一班 | 85 | ||
二班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知一班的复赛成绩的方差是70,请求出二班复试成绩的方差,并说明哪个班成绩比较稳定?