题目内容
24、已知：如图，直线l1∥l2，AB⊥l1垂足为O，BC与l2相交于点D，∠1=43°，求∠2的度数．分析：延长AB交l2于点E，如下图，因为∠2是∠DBE的外角，根据三角形的外角性质求出∠2即可．
或过点B作BF∥l1，利用平行线的性质求出∠2的度数．
或过点B作BF∥l1，利用平行线的性质求出∠2的度数．
解答：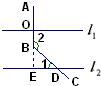
解：解法一：延长AB交l2于点E．∵AB⊥l1，l1∥l2，∴AB⊥l2．
∵∠2是△BED的外角，∴∠2=90°+∠1=90°+43°=133°．
解法二：过点B作BF∥l1，利用平行线的性质求出∠2的度数．
∵l1∥l2，∴BF∥l2，
∴∠ABF=180°-90°=90°，∠FBC=∠1=43°，
∴∠2=∠ABF+∠FBC=90°+43°=133°．
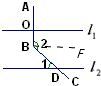
解：解法一：延长AB交l2于点E．∵AB⊥l1，l1∥l2，∴AB⊥l2．∵∠2是△BED的外角，∴∠2=90°+∠1=90°+43°=133°．
解法二：过点B作BF∥l1，利用平行线的性质求出∠2的度数．
∵l1∥l2，∴BF∥l2，
∴∠ABF=180°-90°=90°，∠FBC=∠1=43°，
∴∠2=∠ABF+∠FBC=90°+43°=133°．
点评：熟练掌握平行线的性质及三角形外角的性质．
练习册系列答案
相关题目
（2012•南浔区一模）已知：如图，直线l1：y=ax+2b与直线l2：y=cx+2d的交点坐标为（2，3），则a+b+c+d的值是（ ）
已知：如图，直线l1，l2被l3所截，∠1+∠2=180°．
已知：如图，直线l1与y轴交点坐标为（0，-1），直线l2与x轴交点坐标为（3，0），两直线交点为P（1，1），解答下面问题：
已知：如图，直线l1，l2，l3表示三条相互交叉的公路，现要建一个塔台，若要求它到三条公路的距离都相等，试问：