题目内容
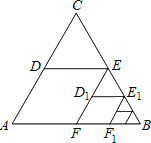
【题目】如图,![]() 是边长为1的等边三角形
是边长为1的等边三角形![]() 取BC边中点E,作
取BC边中点E,作![]() ,
,![]() ,得到四边形EDAF,它的面积记作
,得到四边形EDAF,它的面积记作![]() ;取BE中点
;取BE中点![]() ,作
,作![]() ,
,![]() ,得到四边形
,得到四边形![]() ,它的面积记作
,它的面积记作![]() 照此规律作下去,则
照此规律作下去,则![]() ______.
______.
【答案】![]() 表示为
表示为![]() 亦可
亦可![]()
【解析】分析:
由已知条件易得S△ABC=![]() ,S1=
,S1=![]() S△ABC=
S△ABC=![]() ,S2=
,S2=![]() S△EFB=
S△EFB=![]() S△ABC=
S△ABC=![]() =S1
=S1![]() ,S3=
,S3=![]() S△E1F1B=
S△E1F1B=![]() S△ABC=
S△ABC=![]() =S1
=S1![]() ,……,由此找到规律即可得到所求答案了.
,……,由此找到规律即可得到所求答案了.
详解:
如下图,连接DF,
∵△ABC是边长为1的等边三角形,
∴S△ABC=![]() ,
,
∵点E、F分别是AB、BC边的中点,DE∥AB,EF∥AC,
∴易得DE、EF、DF是△ABC的中位线,
∴S四边形AFED=S1==![]() S△ABC=
S△ABC=![]() ,S△EFB=
,S△EFB=![]() S△ABC=
S△ABC=![]() ,
,
同理可得:S2=![]() S△EFB=
S△EFB=![]() S△ABC=
S△ABC=![]() =S1
=S1![]() ,
,
S3=![]() S△E1F1B=
S△E1F1B=![]() S△ABC=
S△ABC=![]() =S1
=S1![]() ,……,
,……,
∴S2011=S1![]() .
.
故答案为:![]() .
.


练习册系列答案
相关题目
【题目】某农机租赁公司共有50台收割机,其中甲型20台,乙型30台,现将这50台联合收割机派往A,B两地区收割水稻,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800元 | 1600元 |
B地区 | 1600元 | 1200元 |
![]() 设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y元,求y关于x的函数关系式;
设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y元,求y关于x的函数关系式;
![]() 若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;
![]() 农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.
农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.