题目内容
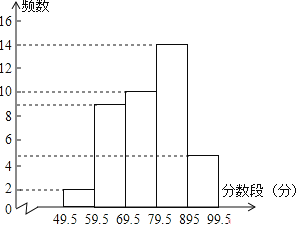
【题目】九(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表,并绘制频数分布直方图.
九(3)班“绿色奥运”知识竞赛成绩频数分布表:
分数段(分) | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~99.5 |
组中值(分) | 54.5 | 64.5 | 74.5 | 84.5 | 94.5 |
频数 | a | 9 | 10 | 14 | 5 |
所占百分比 | 5% | 22.5% | 25.0% | 35.0% | b |
(1)频数分布表中a=______,b=______;
(2)画频数分布直方图;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元,已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.
【答案】(1) 2,0.125;(2)作图见解析;(3) 1050元.
【解析】试题分析:(1)由成绩频数分布表可以看出,b=1-0.05-0.225-0.25-0.35=0.125;由已知组的频数占总数的百分比及频数求出总数,用总数乘0.050求出a的值;
(2)由数据补全直方图;
(3)由表得,有29名同学获得一等奖或二等奖;设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意得关系式15x+10(29-x)=335可求得x的值;再根据关系式50x+30(29-x)可求得获得的奖金.
试题解析:解:(1)频数分布表中,由于![]() ×100%=40(人),则a=40×0.050=2(人),
×100%=40(人),则a=40×0.050=2(人),
b=1-0.05-0.225-0.25-0.35=0.125;
(2)如图所示:
(3)由表得,有29名同学获得一等奖或二等奖,
设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意,得
15x+10(29-x)=335,
解得x=9,
∴50x+30(29-x)=1050.
所以他们得到的奖金是1050元.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案【题目】在中考体育加试中,某班30名男生的跳远成绩如下表:
成绩/m | 1.95 | 2.00 | 2.05 | 2.10 | 2.15 | 2.25 |
人数 | 2 | 3 | 9 | 8 | 5 | 3 |
这些男生跳远成绩的众数、中位数分别是( )
A. 2.10,2.05B. 2.10,2.10C. 2.05,2.10D. 2.05,2.05