Question

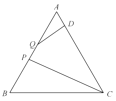
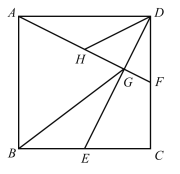
【题目】如图，在边长为4的正方形中，点、分别是、的中点，、交于点，的中点为，连接、．给出下列结论：①；②；③；④．其中正确的结论有________．（请填上所有正确结论的序号）

Answer 1

【答案】①④

【解析】

证明△ADF≌△DCE，再利用全等三角形的性质结合余角的性质得到∠DGF=90°，可判断①，再利用三角形等积法AD×DF÷AF可算出DG，可判断②；再证明∠HDF=∠HFD=∠BAG，求出AG，DH，HF，可判定，可判断④；通过AB≠AG，得到∠ABG和∠AGB不相等，则∠AGB≠∠DHF，可判断③.

解：∵四边形ABCD为正方形，

∴∠ADC=∠BCD=90°，AD=CD，

∵E和F分别为BC和CD中点，

∴DF=EC=2，

∴△ADF≌△DCE（SAS），

∴∠AFD=∠DEC，∠FAD=∠EDC，

∵∠EDC+∠DEC=90°，

∴∠EDC+∠AFD =90°，

∴∠DGF=90°，即DE⊥AF，故①正确；

∵AD=4，DF=CD=2，

∴AF=，

∴DG=AD×DF÷AF=，故②错误；

∵H为AF中点，

∴HD=HF=AF=，

∴∠HDF=∠HFD，

∵AB∥DC，

∴∠HDF=∠HFD=∠BAG，

∵AG=，AB=4，

∴，

∴，故④正确；

∴∠ABG=∠DHF，而AB≠AG，

则∠ABG和∠AGB不相等，

故∠AGB≠∠DHF，

故HD与BG不平行，故③错误；

故答案为：①④.