题目内容
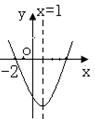
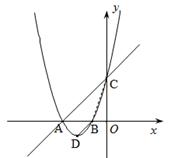
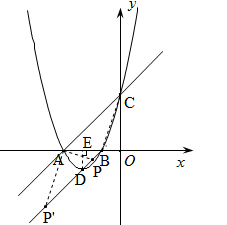
如图,直线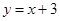 与x轴、y轴分别交于点A、C,经过A、C两点的抛物线
与x轴、y轴分别交于点A、C,经过A、C两点的抛物线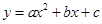 与x轴的负半轴上另一交点为B,且tan∠CBO=3.
与x轴的负半轴上另一交点为B,且tan∠CBO=3.

(1)求该抛物线的解析式及抛物线的顶点D的坐标;
(2)若点P是射线BD上一点,且以点P、A、B为顶点的三角形与△ABC相似,求点P的坐标.
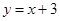 与x轴、y轴分别交于点A、C,经过A、C两点的抛物线
与x轴、y轴分别交于点A、C,经过A、C两点的抛物线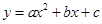 与x轴的负半轴上另一交点为B,且tan∠CBO=3.
与x轴的负半轴上另一交点为B,且tan∠CBO=3.
(1)求该抛物线的解析式及抛物线的顶点D的坐标;
(2)若点P是射线BD上一点,且以点P、A、B为顶点的三角形与△ABC相似,求点P的坐标.
(1)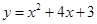 ,D(-2,-1)(2)P的坐标为(
,D(-2,-1)(2)P的坐标为(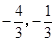 )或(
)或(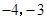 ).
).
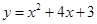 ,D(-2,-1)(2)P的坐标为(
,D(-2,-1)(2)P的坐标为(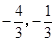 )或(
)或(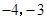 ).
).试题分析:(1)由直线可求得A、C的坐标,再由tan∠CBO=3,可求得B的坐标,用交点式可以求出抛物线解析式,通过配方即可求出顶点D的坐标;
(2)过D作DE⊥AB于E,可以得到∠CAO=∠ABD=45°,直线BD的方程为:
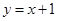 ,表示出PB的长,因为有一对角相等,所以只需要夹这个角的两边对应成比例,即可得到三角形相似,所以有两种情况:
,表示出PB的长,因为有一对角相等,所以只需要夹这个角的两边对应成比例,即可得到三角形相似,所以有两种情况: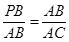 和
和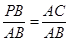 ,分别求出PB,再求出P的坐标即可.
,分别求出PB,再求出P的坐标即可.试题解析:(1)连结BC,由直线
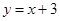 知,点A(-3,0)、C(0,3);∴OC=3,∵tan∠CBO=3,∴OB=1,∴B(-1,0);设
知,点A(-3,0)、C(0,3);∴OC=3,∵tan∠CBO=3,∴OB=1,∴B(-1,0);设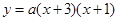 ,把C(0,3)代入得:
,把C(0,3)代入得: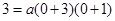 ,解得:
,解得: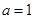 ,∴
,∴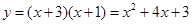 ,∵
,∵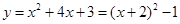 ,∴顶点D(
,∴顶点D(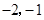 );
);
(2)过D作DE⊥AB于E,∵D (
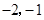 ),B(-1,0),∴DE=1,BE=1,∴∠ABD=45°,∵A(-3,0)、C(0,3),∴OA=OC=3,∴∠CAO=45°,AO=CO=3,∴AC=
),B(-1,0),∴DE=1,BE=1,∴∠ABD=45°,∵A(-3,0)、C(0,3),∴OA=OC=3,∴∠CAO=45°,AO=CO=3,∴AC=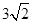 ,∴∠CAO=∠ABD.设直线BD为
,∴∠CAO=∠ABD.设直线BD为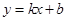 ,把D (
,把D (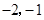 ),B(-1,0)代入得:
),B(-1,0)代入得: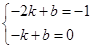 ,解得:
,解得: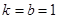 ,∴直线BD为
,∴直线BD为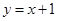 .
.∵点P在射线BD上,∴设P(
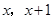 )且
)且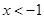 ,则PB=
,则PB=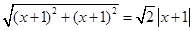 ,∵
,∵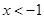 ,∴PB=
,∴PB=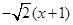 ,∵∠CAO=∠ABD,∴有以下两种情况,可以使以点P、A、B为顶点的三角形与△ABC相似:
,∵∠CAO=∠ABD,∴有以下两种情况,可以使以点P、A、B为顶点的三角形与△ABC相似:①当
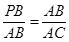 时,即
时,即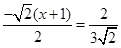 ,解得:
,解得: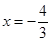 ,∴
,∴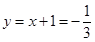 ,∴P(
,∴P(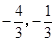 );
);
②当
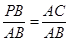 时,即
时,即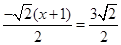 ,解得:
,解得: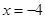 ,∴
,∴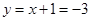 ,∴P(
,∴P(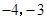 );
);∴点P的坐标为(
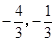 )或(
)或(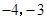 ).
).
练习册系列答案
相关题目
 关于底面的一条边长x
关于底面的一条边长x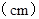 的函数解析式是 .其中x的取值范围是 .
的函数解析式是 .其中x的取值范围是 .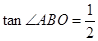 ,抛物线
,抛物线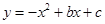 过A、B两点.
过A、B两点.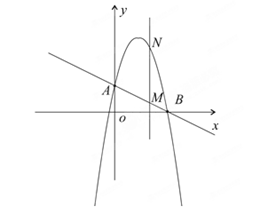
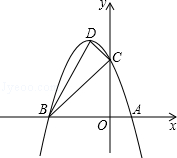
 ,a是常数且
,a是常数且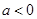 ,下列选项中可能是它大致图像的是( )
,下列选项中可能是它大致图像的是( )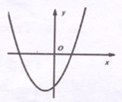

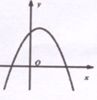

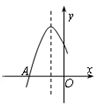
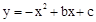 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表: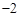
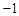
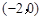 ②抛物线与
②抛物线与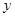 轴的交点为
轴的交点为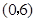
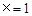 ④在对称轴左侧y随x增大而增大
④在对称轴左侧y随x增大而增大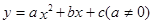 图像如图所示,下列结论:①
图像如图所示,下列结论:①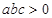 ,②
,②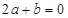 ,③
,③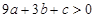 ,④方程
,④方程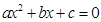 的解是-2和4,⑤不等式
的解是-2和4,⑤不等式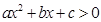 的解集是
的解集是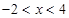 ,其中正确的结论有( )
,其中正确的结论有( )