题目内容
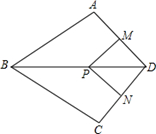
如图,?ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,BC=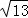 .
.
(1)AC与BD有什么位置关系?为什么?
(2)四边形ABCD是菱形吗?为什么?
(1)垂直,理由见解析 (2)是,理由见解析
解析试题分析:(1)首先根据平行四边形的性质得出CO,BO的长,再利用勾股定理逆定理求出∠BOC=90°,可得AC与BD的位置关系;
(2)菱形的判定方法:对角线互相垂直平分的四边形是菱形,可得答案.
解:(1)∵四边形ABCD是平行四边形,
∴BO=DO=2,AO=CO=3,
∵BC=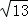 ,
,
∴BO2+CO2=CB2,
∴BD⊥AC,
(2)∵BD⊥AC,
∴四边形ABCD是菱形.
点评:此题主要考查了菱形的判定,平行四边形的性质,以及勾股定理的逆定理的运用,解题的关键是根据条件证出BO2+CO2=CB2.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
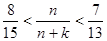 的整数k只有一个,则正整数N的最大值 .
的整数k只有一个,则正整数N的最大值 .