Question

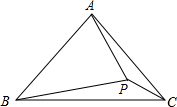
如图，在△ABC中，AB=AC，P为△ABC内一点，且∠BAP=70°，∠ABP=40°，
（1）求证：△ABP是等腰三角形；
（2）连接PC，当∠PCB=30°时，求∠PBC的度数．

Answer 1

（1）证明：在△PAB中，∵∠BAP=70°，∠ABP=40°，
∴∠APB=180°-∠BAP-∠ABP=70°．
∴∠APB=∠BAP=70°．
∴AB=BP，即△ABP是等腰三角形．

（2）过点A作AD⊥BC于D，交CP延长线于O，连接OB，过点B作BE⊥CP于E，则点E在CO延长线上，
即AD是等腰三角形ABC底边上的高，
∴AD是边BC的垂直平分线，
∴OB=OC，
∴∠OBC=∠OCB=30°，
∵BE⊥CE，
∴∠CEB=90°，
∴∠EBC=90°-30°=60°，
∴∠OBE=60°-30°=30°=∠OBD，
在△OEB和△ODB中

∠OEB=∠ODB=90° ∠EBO=∠DBO BO=BO

∴△OEB≌△ODB（AAS），
∴OD=OE，BD=BE，
∵∠BEC=∠ADB=90°，
∴在Rt△ABD和Rt△PBE中

AB=BP BD=BE

，
∴Rt△ABD≌Rt△PBE（HL），
∴∠BAO=∠BPO，AD=PE，
∵OE=OD，
∴AO=PO，
在△AOB和△POB中

AB=BP ∠BAO=∠BPO AO=OP

∴△AOB≌△POB（SAS），
∴∠ABO=∠PBO=

1

2

∠ABP=

1

2

×40°=20°，
∴∠PBC=30°-20°=10°．