题目内容
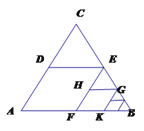
【题目】如图,△ABC是面积为1的等边三角形。取BC边中点E,作ED∥AB,
EF∥AC,得到四边形EDAF,它的面积记做S1;取BE中点G,做GH∥FB,GK∥EF,
得到四边形GHFK,它的面积记作S2.照此规律作下去,
则S2018=__________________.
【答案】![]() 或写成
或写成 ![]()
【解析】分析:根据三角形中位线定理可求出S1的值,进而可得出S2的值,找出规律即可得出S2018的值.
详解:∵E是BC的中点,ED∥AB,
∴DE是△ABC的中位线,
∴DE=![]() AB,
AB,
∴S△DCE=![]() S△ABC.
S△ABC.
同理,S△BEF=![]() S△ABC.
S△ABC.
∴S1=S△ABC-S△DCE-S△BEF=![]() ×S△ABC,
×S△ABC,
同理求得S2=![]() ×S△ABC,
×S△ABC,
…
S2018=![]() ×S△ABC=
×S△ABC=![]() ×1=
×1=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某中学开展“八荣八耻”演讲比赛活动,九![]() 、九
、九![]() 班根据初赛成绩各选出
班根据初赛成绩各选出![]() 名选手参加复赛,两个班各选出的
名选手参加复赛,两个班各选出的![]() 名选手的复赛成绩(满分为
名选手的复赛成绩(满分为![]() 分)如下图所示:
分)如下图所示:
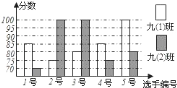
(1)根据上图填写下表:
平均分(分) | 中位数(分) | 众数(分) | |
九 |
|
| |
九 |
|
|
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好?
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好?
(3)如果在每班参加复赛的选手中分别选出![]() 人参加决赛,你认为哪个班的实力更强一些,说明理由.
人参加决赛,你认为哪个班的实力更强一些,说明理由.