题目内容
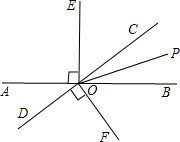
 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线,
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线,
(1)图中除直角外,还有相等的角吗?请写出两对:
①______;②______.
(2)如果∠AOD=40°.
①那么根据______,可得∠BOC=______度.
②因为OP是∠BOC的平分线,所以∠BOP=______度.
③求∠EOF的度数.
解:(1)相等的角有:∠AOD=∠BOC,∠COE=∠BOF,∠BOP=∠COP;
(2)那么根据对顶角相等,可得∠BOC=∠AOD=40度;
②因为OP是∠BOC的平分线,所以∠BOP= ∠BOC=
∠BOC= ×40°=20°;
×40°=20°;
③∵OE⊥AB,OF⊥CD,
∴∠COE=∠BOF=90°-∠BOC=90°-40°=50°,
∴∠EOF=∠COE+∠BOC+∠BOF=50°+40°+50°=140°.
故答案为:(1)∠AOD=∠BOC,∠COE=∠BOF;(2)对顶角相等,40,20.
分析:(1)根据同角的余角相等,对顶角相等以及角平分线的定义解答即可;
(2)①根据对顶角相等解答;
②根据角平分线的定义解答;
③先根据垂线的定义求出∠COE和∠BOF,再根据∠EOF=∠COE+∠BOC+∠BOF进行计算即可得解.
点评:本题考查了垂线的定义,角平分线的定义,对顶角相等的性质,是基础题,熟记性质与概念并准确识图是解题的关键.
(2)那么根据对顶角相等,可得∠BOC=∠AOD=40度;
②因为OP是∠BOC的平分线,所以∠BOP=
 ∠BOC=
∠BOC= ×40°=20°;
×40°=20°;③∵OE⊥AB,OF⊥CD,
∴∠COE=∠BOF=90°-∠BOC=90°-40°=50°,
∴∠EOF=∠COE+∠BOC+∠BOF=50°+40°+50°=140°.
故答案为:(1)∠AOD=∠BOC,∠COE=∠BOF;(2)对顶角相等,40,20.
分析:(1)根据同角的余角相等,对顶角相等以及角平分线的定义解答即可;
(2)①根据对顶角相等解答;
②根据角平分线的定义解答;
③先根据垂线的定义求出∠COE和∠BOF,再根据∠EOF=∠COE+∠BOC+∠BOF进行计算即可得解.
点评:本题考查了垂线的定义,角平分线的定义,对顶角相等的性质,是基础题,熟记性质与概念并准确识图是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.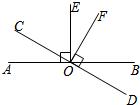 8、如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.则图中除了直角相等外,还有相等的角,请写出三对:
8、如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.则图中除了直角相等外,还有相等的角,请写出三对: 10、如图,直线AB与CD相交于O点,且∠COE=90°,则与∠EOA互余的角有
10、如图,直线AB与CD相交于O点,且∠COE=90°,则与∠EOA互余的角有 如图,直线AB与CD相交于点O,∠AOC=65°,则∠DOB=
如图,直线AB与CD相交于点O,∠AOC=65°,则∠DOB=