Question

【题目】已知О是直线AB上的一点，，OE平分．

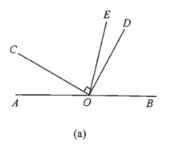
（1）在图（a）中，若，求的度数；

（2）在图（a）中，若，直接写出的度数（用含的代数式表示）

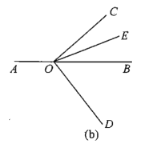
（3）将图（a）中的绕顶点O顺时针旋转至图（b）的位置．

①探究和的度数之间的关系，直接写出结论；

②在的内部有一条射线OF，满足：，试确定与的度数之间的关系，并说明理由．

Answer 1

【答案】（1）15°；（2）；（3）①；②，理由详见解析．

【解析】

（1）由已知可求出∠BOC=180°-∠AOC=150°，再由∠COD是直角，OE平分∠BOC求出∠DOE的度数；
（2）由（1）中的证明方法可得出结论∠DOE=∠AOC，从而用含的代数式表示出∠DOE的度数；
（3）①由∠COD是直角，OE平分∠BOC可得出∠COE=∠BOE=90°-∠DOE，则得∠AOC=180°-∠BOC=180°-2∠COE=180°-2（90°-∠DOE），从而得出∠AOC和∠DOE的度数之间的关系；
②设，，根据①中结论以及已知，得出，从而得出结论．

（1）∵，，

∴．

∵OE平分，

∴．

∵，

∴

（2）．

∵，，

∴．

∵OE平分，

∴

∵，

∴．

（3）①．

∵OE平分，

∴．

∵，∴．

∵，

∴．

∴．

即．

②．

理由：设，，

由①可知，．

∴．

∵，

∴．

∴．

∵，

∴．

∴．

即．