题目内容
有一个锐角是30°的直角三角形中,斜边长为1cm,则斜边上的高为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:先根据在直角三角形中30°所对的边是斜边的一半,即可求得30°所对的直角边的长度,再利用勾股定理求得另一直角边的长度;根据角的正弦值以及另一直角边的长度即可求得斜边上的高.
解答:解:∵在直角三角形中30°所对的边是斜边的一半,
∴30°所对的直角边=
cm;
则根据勾股定理可知,另一直角边=
=
cm;
根据在直角三角形中30°所对的边是斜边的一半可得,
斜边上的高=
×另一直角边的长度=
cm.
∴30°所对的直角边=
| 1 |
| 2 |
则根据勾股定理可知,另一直角边=
1-(
|
| ||
| 2 |
根据在直角三角形中30°所对的边是斜边的一半可得,
斜边上的高=
| 1 |
| 2 |
| ||
| 4 |
点评:熟练掌握好边角之间的关系是解决本题的关键.

练习册系列答案
相关题目
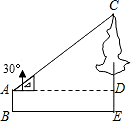 如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )A、(
| ||||||
B、(5
| ||||||
C、
| ||||||
| D、4m |
 如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
 m B、
m B、 m C、
m C、 m
D、4 m
m
D、4 m