题目内容
【题目】如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.
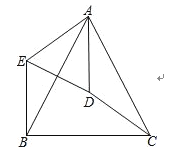
(1)求证:△AED∽△ABC;
(2)连接BD,判断四边形AEBD的形状并证明.
【答案】(1)△AED∽△ABC;
(2)四边形AEBD是菱形.
【解析】
试题分析:(1)由旋转性质可得∠DAE=∠CAB、AE=AD,结合AB=AC根据![]() 且∠DAE=∠CAB可证得;
且∠DAE=∠CAB可证得;
(2)由三角形外心可得DB=DA=DC,结合△ADC≌△AEB知DB=DA=BE=AE,即可判定四边形AEBD的形状.
试题解析:(1)∵△ADC 绕点A顺时针旋转得到△AEB,
∴△ADC≌△AEB.
∴∠BAE=∠CAD,AE=AD.
∴∠DAE=∠CAB.
∵AB=AC,
∴![]() .
.
∴△AED∽△ABC.
(2)四边形AEBD是菱形.
∵D是△ABC的外心,
∴DB=DA=DC.
又∵△ADC≌△AEB,
∴AE=AD,BE=DC.
∴DB=DA=BE=AE.
∴四边形AEBD是菱形.

练习册系列答案
相关题目